Геометрия формирования изображений

Здесь с геометрической точки зрения объясняются основы формирование изображения.

В частности, рассматривается математика, стоящая за тем, как точка в 3D‑изображении проецируется на плоскость изображения.

Статья по своей природе не математическая и предназначена исключительно для новичков. Тем не менее, что такое перемножение матриц знать надо.

Проблема

Для понимания задачи, предположим, что у нас есть камера, установленная в комнате.

Зная, что в комнате есть точка \mathbf{P} в трехмерном пространстве (3D‑точка, Декартова система координат^એ), мы хотим найти координаты пикселя (u, v) этой 3D‑точки на снимке, сделанном камерой.

В этом контексте есть три системы координат. Давайте с ними разберёмся.

1. Мировая система координат

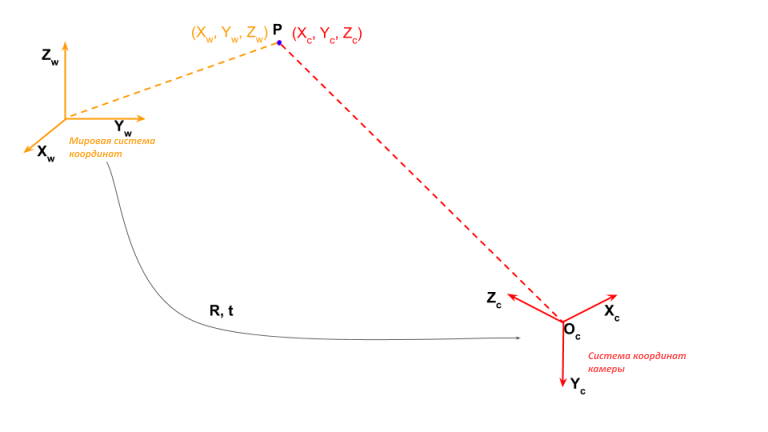
Чтобы определить расположение точек в помещении, нам нужно сначала определить систему координат этого помещения. Это требует знания двух вещей:

• начало координат: можно произвольно назвать любой угол комнаты началом (0, 0, 0).
• направление осей X, Y, Z: оси X и Y можно направить в плоскости пола вдоль двух стенок, а ось Z вдоль вертикального угла стены.

Принимая во внимание всё это, можно найти три координаты любой точки в комнате, измерив расстояние от неё до начала координат по осям X, Y и Z.

Эта система координат, связанная с комнатой, называется мировой системой координат. На рисунке 1 она показан осями оранжевого цвета. Мы будем использовать жирный шрифт (например, X_w), чтобы показать ось, и обычный шрифт, чтобы показать координату точки (например, X_w).

Давайте рассмотрим точку Р в этой комнате. В мировой системе координат координаты Р задаются по осям (X_w, Y_w, Z_w). Вы можете найти X_w, Y_w, и Z_w координаты этой точки, просто измеряя расстояние от этой точки до начала координат по трем осям.

2. Система Координат Камеры

А теперь давайте поставим камеру в комнате.

Снимать будем этой камерой и поэтому нас интересует связанная с ней трехмерная система координат.

Если бы мы поместили камеру в начало координат комнаты и выровняли ее таким образом, чтобы ее оси X, Y и Z совпадали с осями X_w, Y_w и Z_w комнаты, то эти две системы координат были бы одинаковыми.

Однако, это вряд ли возможно на практике. Мы хотели бы поставить камеру в любом месте и она должна видеть любое месте. Поэтому нам нужно найти связь между координатами 3D‑комнаты (т.е. мира) и координатами 3D‑камеры.

Допустим, наша камера стоит где‑то произвольно (t_X, t_Y, t_Z) в комнате. На техническом жаргоне мы можем перевести координаты камеры по (t_X, t_Y, t_Z) по отношению к мировым координатам.

Камера может также смотреть куда угодно. Другими словами, можно сказать, что камера вращается относительно мировой системы координат.

Вращение в 3D определяется тремя параметрами — тангаж, рыскание и крен. Образно это представляется движением руки от локтя: вверх‑вниз — тангаж, слева‑направо — рыскание, вращение кулака — крен.

Однако часто для математической манипуляции удобно задавать вращение в виде матрицы 3 × 3. Теперь вы можете подумать, что матрица 3 × 3 имеет 9 элементов и, следовательно, 9 параметров, но у вращения только 3 параметра. И это правильно, именно поэтому любая произвольная матрица 3 × 3 не является матрицей вращения. Не вдаваясь в детали, давайте пока просто узнаем, что матрица вращения имеет только три степени свободы, хотя она имеет 9 элементов.

Вернемся к нашей первоначальной проблеме. Мировая координата и координаты камеры связаны матрицей вращения \mathbf{R} и вектором перемещения 3 элементов \mathbf{t}

Что это значит?

Это значит, что точка \mathbf{P}, имеющая координаты (X_w, Y_w, Z_w) в мировой системе координат, в системе координат камеры будет иметь другие значения (X_c, Y_c, Z_c). Система координат камеры на рисунке изображена красным цветом.

Эти координаты связаны следующим уравнением.

\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}= \mathbf{R} \begin{bmatrix}X_w\\Y_w\\Z_w\end{bmatrix} + \mathbf{t}

Обратите внимание, что представление вращения в виде матрицы позволило нам выполнять вращение простым умножением матрицы вместо утомительной манипуляции символами, требуемой в других представлениях, таких как тангаж, рыскание, крен. Я надеюсь, что это поможет вам понять, почему мы описываем вращение, используя матрицы.

Иногда приведенное выше выражение пишется в более компактной форме. Вектор перевода 3 × 1 добавляется в виде столбца в конец матрицы вращения 3 × 3, чтобы получить матрицу 3 × 4, называемую внешней матрицей .

\begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}= \begin{bmatrix} \mathbf{R} / \mathbf{t} \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\ \ Z_w \\ 1 \end{bmatrix}

где, внешняя матрица \mathbf{P} задается с помощью

\mathbf{P} = \begin{bmatrix} \mathbf{R} / \mathbf{t} \end{bmatrix}

Однородные координаты: в проективной геометрии мы часто работаем с забавным представлением координат, где к координатам добавляется дополнительное измерение. Трехмерная точка (X, Y, Z) в декартовых координатах может быть записана как (X, Y, Z, 1) в однородных координатах. В более общем случае точка в однородной координате (X, Y, Z, W) совпадает с точкой (X / W, Y/ W, Z / W) в декартовых координатах. Однородные координаты позволяют нам представлять бесконечные величины, используя конечные числа. Например, точку на бесконечности можно представить в виде (1, 1, 1, 0) в однородных координатах. Вы можете заметить, что мы использовали однородные координаты в уравнении 2 для представления мировых координат.

3. Система координат изображения

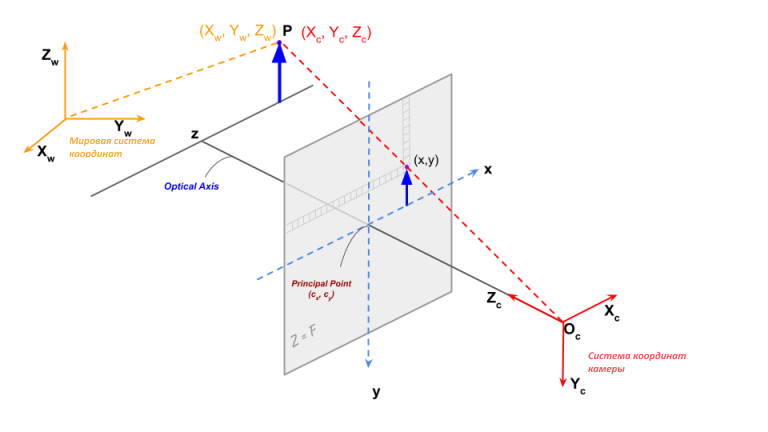
После того, как мы получим точку в трехмерной системе координат камеры, применяя вращение и перевод к точкам мировых координат, мы находимся в положении, когда можем спроецировать точку на плоскости изображения для вычисления местоположение точки на изображении.

На изображении выше мы смотрим на точку \mathbf{P} с координатами (X_c, Y_c, Z_c) в системе координат камеры. Напомним только, что если бы мы не знали координаты этой точки в системе координат камеры, мы могли бы преобразовать ее координаты в мировой системе координат, используя внешнюю матрицу, чтобы получить координаты в системе координат камеры, используя уравнение 2.

Рисунок 2, показывает проекцию камеры в случае простой камеры с контактным отверстием.

Оптический центр^એ (ось наблюдения) представлен с помощью O_c. В действительности на плоскости формируется перевернутое изображение. Для математического удобства мы просто делаем все вычисления, как будто плоскость изображения находится перед оптическим центром, потому что изображение, считанное с матрицы, может быть тривиально повернуто на 180 градусов, чтобы компенсировать инверсию. На практике даже этого не требуется. Всё еще проще: реальная светочувствительная матрица камеры просто читается начиная самого нижнего ряда в обратном порядке (справа налево), а затем снизу вверх для каждого ряда. Такой метод автоматически формируется правильное изображение и по вертикали и по горизонтали. Так что на практике нет необходимости переворачивать изображение.

Плоскость изображения размещается на расстоянии \mathbf{\phi} (фокусное расстояние^એ) от оптического центра.

Используя геометрию средней школы (подобные треугольники), мы можем показать проектное изображение (x, y) 3D‑точки (X_c, Y_c, Z_c), заданной.

x = f \frac{X_c}{Z_c} \\ y = f \frac{Y_c}{Z_c}

Приведенные выше два уравнения можно переписать в матричной форме следующим образом:

\begin{bmatrix}x'\\y'\\z'\end{bmatrix} = \begin{bmatrix}f&0&0\\0&f&0\\0&0&1\end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}

Матрица \mathbf{К}, показанная ниже, называется внутренней матрицей и содержит внутренние параметры камеры.

\mathbf{K} = \begin{bmatrix}f&0&0\\0&f&0\\0&0&1\end{bmatrix}

Приведенная выше простая матрица показывает только фокусное расстояние.

Однако, пиксели в светочувствительной матрице камеры могут быть не квадратными, и поэтому мы можем иметь два разных фокусных f_x и f_y расстояния.

Оптический центр (c_x, c_y) камеры может не совпадать с центром системы координат изображения.

Кроме того, может наблюдаться небольшой перекос \mathbf{\gamma} между осями \mathbf{x} и \mathbf{y} датчика камеры.

Учитывая это все, матрицу камеры нужно переписать так:

\mathbf{K} = \begin{bmatrix}f_x&\gamma&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}

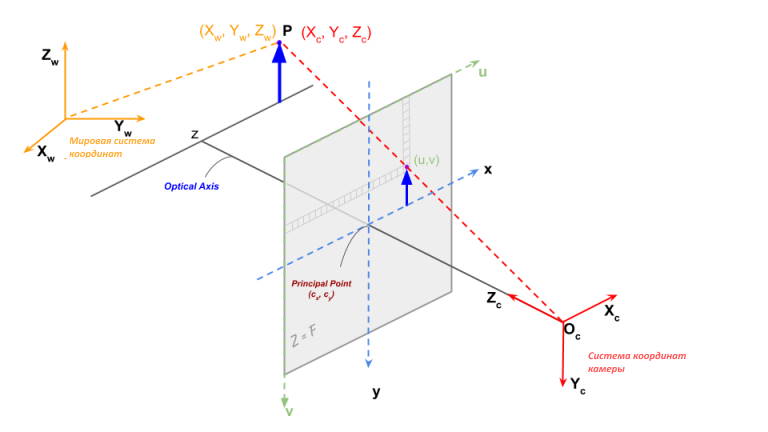
В приведенном выше уравнении координаты \mathbf{x} и \mathbf{y} пикселей находятся относительно центра изображения. Однако при работе с изображениями источник находится в верхнем левом углу изображения.

Давайте представим координаты изображения по (u, v).

\begin{bmatrix}u'\\v'\\w'\end{bmatrix} = \begin{bmatrix}f_x&\gamma&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}

где,

u = \frac{u'}{w'} \\ v = \frac{v'}{w'}

Итого

Проецирование трехмерной точки в мировой системе координат на пиксельные координаты камеры выполняется в три этапа.

1. Трехмерная точка преобразуется из мировых координат в координаты камеры с помощью внешней матрицы, которая состоит из вращения и перемещения между двумя системами координат.
2. Новая трехмерная точка в системе координат камеры проецируется на плоскость изображения с помощью встроенной матрицы, которая состоит из внутренних параметров камеры, таких как фокусное расстояние, оптический центр и т. д.

В следующем посте этой серии мы узнаем о калибровке камеры и о том, как выполнять ее с помощью функции OpenCV.

Оригинал (англ.): Geometry of Image Formation