Урок 1. Распознавание изображений и обнаружение объектов

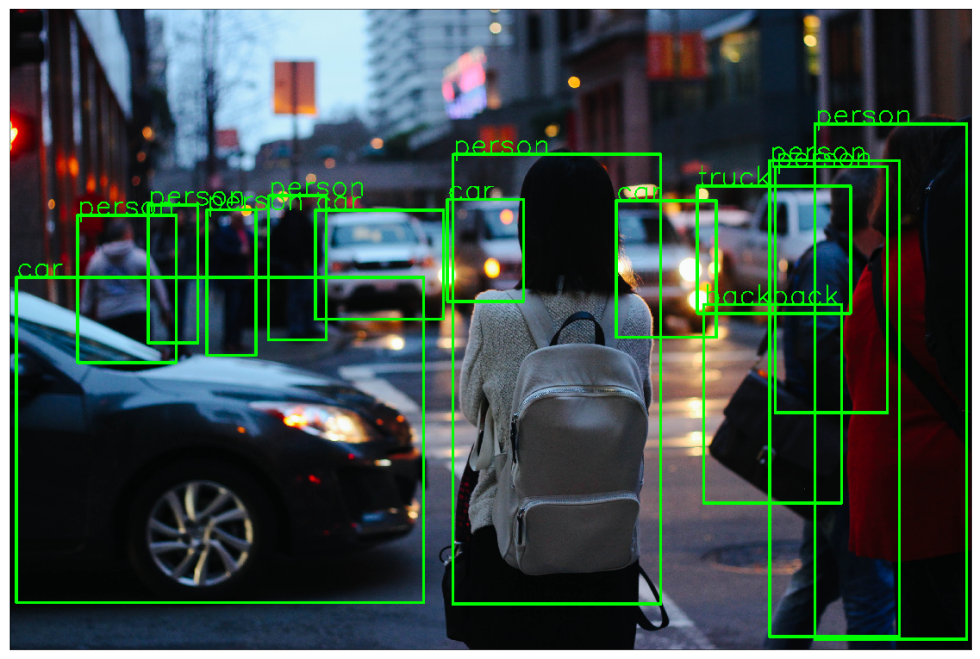
Начинаю серию уроков (мини-курс) о распознавании изображений и обнаружении объектов.

В первой части краткое объяснение понятий распознавание изображений с использованием традиционных методов компьютерного зрения. Я называю методы, не основанные на глубоком обучении, традиционными методами компьютерного зрения, потому что они быстро заменяются методами, основанными на глубоком обучении. Тем не менее, традиционные подходы к компьютерному зрению используются по-прежнему во многих приложениях. Многие из этих алгоритмов также доступны в библиотеках компьютерного зрения, таких как OpenCV^એ, и очень хорошо работают «из коробки».

Мини-курс, который я пишу, будет состоять из 8 уроков по приблизительно следующей тематике:

1. Распознавание изображений с использованием традиционных методов компьютерного зрения
2. Гистограмма направленных градиентов
3. Пример кода для распознавания изображений
4. Обучение лучшему детектору глаза
5. Обнаружение объектов с использованием традиционных методов компьютерного зрения
6. Как обучить и протестировать собственный детектор объектов OpenCV
7. Распознавание изображений с использованием глубокого обучения
   • Введение в нейронные сети
   • Понимание нейронных сетей с прямой связью
   • Распознавание изображений с использованием сверточных нейронных сетей
8. Обнаружение объектов с использованием глубокого обучения

Краткая история распознавания изображений и обнаружения объектов

Наша история начинается в 2001 году; В этом году Пол Виола и Майкл Джонс изобрели эффективный алгоритм распознавания лиц. Их демонстрация, показывающая, что лица обнаруживаются в реальном времени на веб-камере, была самой ошеломляющей демонстрацией компьютерного зрения и его потенциала на то время. Скоро, алгоритм был реализован в OpenCV^એ, и метод Виолы — Джонса^એ стал синонимом обнаружение лиц.

Каждые несколько лет появляется новая идея, которая заставляет людей делать паузу и принимать к сведению. В области обнаружения объектов эта идея появилась в 2005 году в статье Навнит Далала и Билла Триггса. Их дескриптор функции, гистограмма направленных градиентов^એ (HOG), значительно превзошел существующие алгоритмы обнаружения пешеходов.

Примерно каждые десять лет появляется новая идея, настолько эффективная и мощная, что вы отказываетесь от всего, что было до нее, и всем сердцем принимаете новое. Глубокое обучение^એ — идея этого десятилетия. Алгоритмы глубокого обучения существуют уже давно, но они стали мейнстримом в компьютерном зрении благодаря его оглушительному успеху на конкурсе ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2012 года. В этом конкурсе алгоритм, основанный на глубоком обучении Алекса Крижевского, Ильи Суцкевер,и Джеффри Хинтон потрясли мир компьютерного зрения с поразительной точностью 85% — на 11% лучше, чем алгоритм, занявший второе место! В ILSVRC 2012 это была единственная запись, основанная на глубоком обучении. В 2013, все победившие работы были основаны на глубоком обучении, и в 2015 году несколько алгоритмов под общим названием Свёрточная нейронная сеть^એ (CNN) превзошли уровень естественного распознавания человеком 95%.

При таком огромном успехе в распознавании изображений обнаружение объектов на основе глубокого обучения было неизбежным. Такие методы, как Faster R-CNN, производят челюсти. Отбрасывание результатов по нескольким классам объектов. Мы узнаем об этом в следующих публикациях, но пока имейте в виду, что если вы не изучили алгоритмы распознавания изображений и обнаружения объектов на основе глубокого обучения для своих приложений, вы можете упустить огромную возможность получить лучшие результаты.

Теперь готовы вернуться к основной цели этого поста — разобраться в распознавании изображений с помощью традиционных методов компьютерного зрения.

Распознавание изображений (также известное как классификация изображений)

Алгоритм распознавания изображений (также известный как классификатор изображений) принимает изображение (или фрагмент изображения) в качестве входных данных и выводит то, что содержит изображение. Другими словами, вывод — это метка класса (например, «кошка», «собака», «таблица» и т.д.). Как алгоритм распознавания изображений узнает содержимое изображения? Хорошо, вам нужно обучить алгоритм, чтобы узнать различия между разными классами. Если вы хотите найти кошек на изображениях, вам необходимо обучить алгоритм распознавания изображений с тысячами изображений кошек и тысячами изображений фона, которые не содержат кошек. Разумеется, подобный алгоритм может понимать только те объекты/классы, которые он знает.

Чтобы упростить задачу, в этом посте мы сосредоточимся только на двухклассовых (бинарных) классификаторах. Вы можете подумать, что это очень ограничивающее предположение, но имейте в виду, что многие популярные детекторы объектов (например, детектор лиц и детектор пешеходов) имеют под капотом бинарный классификатор. Например, внутри детектора лиц находится классификатор изображений, который сообщает, является ли участок изображения лицом или фоном.

Анатомия классификатора изображений

На следующей диаграмме показаны этапы работы традиционного классификатора изображений.

Интересно, что многие традиционные алгоритмы классификации изображений компьютерного зрения следуют этому конвейеру, в то время как алгоритмы, основанные на глубоком обучении, полностью обходят этап извлечения признаков. Давайте рассмотрим эти шаги более подробно.

Шаг 1: предварительная обработка

Часто входное изображение предварительно обрабатывается для нормализации эффектов контрастности и яркости. Очень распространенный этап предварительной обработки — вычесть среднее значение интенсивности изображения и разделить его на стандартное отклонение. Иногда гамма-коррекция дает немного лучшие результаты. При работе с цветными изображениями преобразование цветового пространства (например, цветовое пространство RGB в LAB) может помочь получить лучшие результаты.

Обратите внимание, что я не прописываю, какие шаги предварительной обработки являются хорошими. Причина в том, что никто заранее не знает, какой из этих шагов предварительной обработки даст хорошие результаты. Вы пробуете несколько разных, и некоторые из них могут дать немного лучшие результаты. Вот абзац из Далала и Триггса

Мы оценили несколько представлений входных пикселей, включая цветовые пространства в оттенках серого, RGB и LAB, опционально со степенным (гамма) выравниванием. Эти нормализации имеют лишь умеренное влияние на производительность, возможно, потому, что последующая нормализация дескриптора дает аналогичные результаты. Мы используем информацию о цвете, когда она доступна. Цветовые пространства RGB и LAB дают сравнимые результаты, но ограничение оттенками серого снижает производительность на 1,5% при 10–4 кадрах в секунду. Гамма-сжатие с квадратным корнем для каждого цветового канала улучшает производительность при низких значениях FPPW (на 1% при 10–4 кадрах в секунду), но логарифмическое сжатие слишком велико и ухудшает его на 2% при 10–4 кадрах в секунду.

Как вы видете, авторы не знали заранее, какую предварительную обработку использовать. Они делали разумные предположения и использовали метод проб и ошибок.

В рамках предварительной обработки входное изображение или фрагмент изображения также обрезаются и изменяются до фиксированного размера. Это важно, потому что следующий шаг, извлечение признаков, выполняется на изображении фиксированного размера.

Шаг 2: извлечение признаков

Входное изображение содержит слишком много дополнительной информации, которая не нужна для классификации. Следовательно, первым шагом в классификации изображений является упрощение изображения путем извлечения важной информации, содержащейся в изображении, и исключения остальной части. Например, если вы хотите найти на изображениях пуговицы рубашек и пальто, то заметите значительные различия в значениях пикселей RGB. Однако, запустив детектор краев изображения, можно упростить изображение. Вы все еще можете легко различить круглую форму кнопок на этих изображениях краев, и поэтому мы можем сделать вывод, что обнаружение краев сохраняет важную информацию, отбрасывая несущественную информацию. Этот шаг называется извлечением признаков. В традиционных подходах к компьютерному зрению разработка этих функций имеет решающее значение для производительности алгоритма. Оказывается, мы можем сделать намного лучше, чем простое обнаружение краев, и найти функции, которые намного надежнее. В нашем примере с пуговицами рубашки и пальто, хороший детектор функций будет не только фиксировать круглую форму кнопок, но и информацию о том, чем кнопки отличаются от других круглых объектов, таких как автомобильные шины.

Некоторыми хорошо известными функциями, используемыми в компьютерном зрении, являются функции типа Хаара, представленные Виолой и Джонсом, гистограмма направленных градиентов (HOG), Масштабно-инвариантная трансформация признаков^એ Scale-Invariant Feature Transform (SIFT), ускорение надежного элемента Speeded Up Robust Feature (SURF) и т.д.

В качестве конкретного примера давайте посмотрим на извлечение признаков с помощью гистограммы ориентированных градиентов (HOG).

Histogram of Oriented Gradients (HOG) или гистограмма направленного градиента

Алгоритм извлечения признаков преобразует изображение фиксированного размера в вектор признаков фиксированного размера. В случае обнаружения пешеходов дескриптор объекта HOG вычисляется для фрагмента изображения размером 64 \times 128 и возвращает вектор размером 3780. Обратите внимание, что исходный размер этого фрагмента изображения был 64 \times 128 \times 3 = 24,576, который сокращен до 3780 дескриптором HOG.

HOG основан на идее, что внешний вид локального объекта может быть эффективно описан распределением (гистограммой) направлений краев (направленных градиентов). Шаги по вычислению дескриптора HOG для изображения размером 64 × 128 перечислены ниже.
Расчет градиента: вычисление градиентов x и y изображений и, исходя из исходного изображения. Это можно сделать, отфильтровав исходное изображение следующими ядрами.

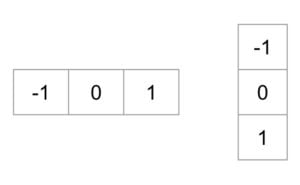
1. Используя изображения градиента и, можно вычислить величины g_x и g_y направления градиента, используя следующие уравнения:

   g = \sqrt{g_x^2 + g_y^2}

   \theta = \arctan{\dfrac{g_x}{g_y}}

   Вычисленные градиенты «беззнаковые» и, следовательно, лежат в диапазоне от 0 до 180 градусов.

2. Ячейки: разделите изображение на ячейки размером 8 \times 8.
3. Вычисление гистограммы градиентов в этих ячейках 8 \times 8: для каждого пикселя в ячейке 8 \times 8 мы знаем градиент (величину и направление), и, следовательно, у нас есть 64 величины и 64 направления, то есть 128 чисел. Гистограмма этих градиентов даст более удобное и компактное представление. Затем мы преобразуем эти 128 чисел в 9‑биновую гистограмма (т.е. 9 чисел). Бины гистограммы соответствуют направлениям градиентов 0, 20, 40… 160 градусов. Каждый пиксель голосует за одну или две ячейки гистограммы. Если направление градиента в пикселе равно 0, 20, 40… или 160 градусам, голос, равный величине градиента, передается пикселем в ячейку. Пиксель, у которого направление градиента не совсем 0, 20, 40… 160 градусов, разделяет свой голос между двумя ближайшими ячейками в зависимости от расстояния от ячейки. Например. Пиксель с величиной градиента 2 и углом 20 градусов будет голосовать за вторую ячейку со значением 2. С другой стороны,пиксель с градиентом 2 и углом 30 будет голосовать за 1 как за второй интервал (соответствующий углу 20), так и за третий интервал (соответствующий углу 40).
4. Нормализация блока: гистограмма, вычисленная на предыдущем шаге, не очень устойчива к изменениям освещения. Умножение интенсивности изображения на постоянный коэффициент также масштабирует значения бина гистограммы. Чтобы противостоять этим эффектам, мы можем нормализовать гистограмму, т.е. представить гистограмму как вектор из 9 элементов, разделив каждый элемент на величину этого вектора. В исходной статье HOG эта нормализация выполняется не по ячейке 8 \times 8, которая произвела гистограмму, а по блокам 16 \times 16. Идея та же самая, но теперь вместо вектора из 9 элементов у вас есть вектор из 36 элементов.
5. Вектор признаков: на предыдущих шагах мы выяснили, как вычислить гистограмму по ячейке 8 \times 8, а затем нормализовать ее по блоку 16 \times 16. Чтобы вычислить окончательный вектор признаков для всего изображения, блок 16 \times 16 перемещается с шагом 8 (т.е. 50% перекрытие с предыдущим блоком), и 36 чисел (соответствующих 4 гистограммам в блоке 16 \times 16), вычисленные на каждом шаге, объединяются для получения окончательного вектора признаков. Какова длина последнего вектора?
   Входное изображение имеет размер 64 \times 128 пикселей, и мы перемещаем 8 пикселей за раз. Следовательно, мы можем сделать 7 шагов в горизонтальном направлении и 15 шагов в вертикальном направлении, что в сумме составляет 7 \times 15 = 105 шагов. На каждом шаге мы вычисляли 36 чисел, что составляет длину конечного вектора 105 \times 36 = 3\:780.

Шаг 3: алгоритм классификации (подробнее)

В предыдущем разделе мы узнали, как преобразовать изображение в вектор признаков. В этом разделе мы узнаем, как алгоритм классификации принимает этот вектор признаков в качестве входных данных и выводит метку класса (например, кошка или фон).

Прежде чем алгоритм классификации сможет творить чудеса, нам нужно обучить его, показывая тысячи примеров кошек и фонов. Различные алгоритмы обучения работают по‑разному, но общий принцип заключается в том, что алгоритмы обучения рассматривают векторы признаков как точки в пространстве более высоких измерений, и попытайтесь найти плоскости/поверхности, которые разделяют пространство более высоких измерений таким образом, что все примеры, принадлежащие к тому же классу, находятся на одной стороне плоскости/поверхности.

Чтобы упростить задачу, давайте более подробно рассмотрим один алгоритм обучения, который называется Support Vector Machines (SVM) или метод опорных векторов^એ. Как работает метод опорных векторов (SVM) для классификации изображений?

Метод опорных векторов — один из самых популярных алгоритмов контролируемой двоичной классификации. Хотя идеи, используемые в SVM, существуют с 1963 года, текущая версия была предложена в 1995 году Кортесом и Вапником.

На предыдущем шаге мы узнали, что дескриптор HOG изображения является вектором признаков длиной 3 780. Мы можем думать об этом векторе как о точке в 3 780-мерном пространстве. Визуализировать пространство большого измерения невозможно, поэтому немного упростим ситуацию и представим, что вектор признаков был двухмерным.

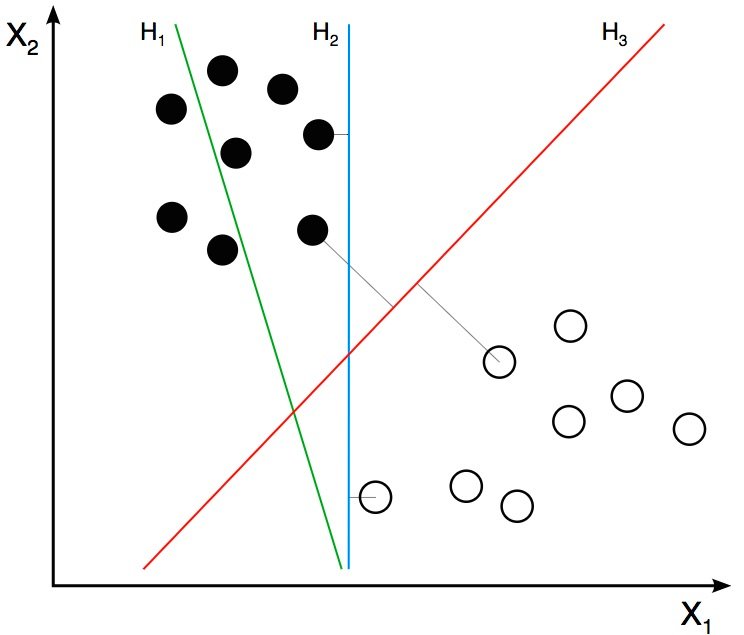
В нашем упрощенном мире теперь у нас есть 2D-точки, представляющие два класса (например, кошки и фон). На изображении выше два класса представлены двумя разными типами точек. Все черные точки принадлежат одному классу, а белые точки — другому классу. Во время тренировки мы предоставляем алгоритм с множеством примеров из двух классов. Другими словами, мы сообщаем алгоритму координаты двумерных точек, а также то, какая точка — черная или белая.

Различные алгоритмы обучения выясняют, как по-разному разделить эти два класса. Линейная SVM пытается найти лучшую линию, разделяющую два класса. На рисунке выше H1, H2 и H3 — это три линии в этом двухмерном пространстве. H1 не разделяет два класса и поэтому не является хорошим классификатором. H2 и H3 разделяют два класса, но интуитивно кажется, что H3 — лучший классификатор, чем H2, потому что H3, кажется, разделяет два класса более четко. Почему? Потому что H2 находится слишком близко к некоторым черным и белым точкам. С другой стороны, H3 выбирается таким образом, чтобы он находился на максимальном расстоянии от членов двух классов.

Учитывая 2D-функции на рисунке выше, SVM найдет для вас линию H3. Если вы получите новый двумерный вектор признаков, соответствующий изображению, которого алгоритм никогда раньше не видел, то можете просто проверить, на какой стороне линии лежит точка, и присвоить ей соответствующую метку класса. Если ваши векторы признаков находятся в 3D, SVM найдет подходящую плоскость, которая максимально разделяет два класса. Как вы, возможно, догадались, если ваш вектор признаков находится в 3 780‑мерном пространстве, SVM найдет соответствующую гиперплоскость.

Оптимизация SVM

Пока все хорошо, но я знаю, что у вас есть один важный вопрос, на который нет ответа. Что, если объекты, принадлежащие двум классам, нельзя разделить с помощью гиперплоскости? В таких случаях, SVM по-прежнему находит лучшую гиперплоскость, решая задачу оптимизации, которая пытается увеличить расстояние гиперплоскости от двух классов, одновременно пытаясь обеспечить правильную классификацию многих обучающих примеров. Этот компромисс контролируется параметром C. Когда значение C мало, выбирается гиперплоскость с большим запасом за счет большего числа ошибочных классификаций. И наоборот, когда C велико, выбирается гиперплоскость меньшего поля, которая пытается правильно классифицировать гораздо больше примеров.

Теперь вы можете быть сбиты с толку, какое значение выбрать для C. Выберите то значение, которое лучше всего работает на тестовом наборе, которого не было в обучающей выборке.

Image Recognition and Object Detection: Part 1