Нейронные сети для начинающих: взгляд с высоты птичьего полета

В этой статье я хочу взглянуть на нейронные сети с высоты птичьего полета. Этот пост написан для абсолютных новичков, которые не знают о них ничего, от слова совсем, но пытаются понять, что такое машинное и глубокое обучение.

Будем милыми и не навязчивыми, а, главное, без математики.

Нейронные сети как черный ящик

Начнем с рассмотрения нейронных сетей как волшебного черного ящика. Вы не знаете, что внутри черного ящика. Все, что вы знаете, это то, что у него один вход и три выхода. Входными данными является изображение любого размера, цвета, вида и т.д. Три выхода — это числа от 0 до 1. Выходы помечены как «Кот», «Собака» и «Прочее». Сумма трех чисел всегда равна 1.

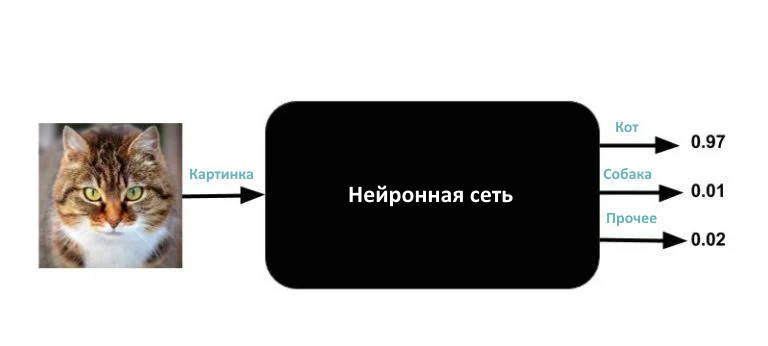
Что такое выход нейронной сети?

Магия, которую он творит, очень проста. Если вы введете изображение в черный ящик, он выведет три числа. Идеальная нейронная сеть будет выводить (1, 0, 0) для кошки, (0, 1, 0) для собаки и (0, 0, 1) для всего, что не является кошкой или собакой. Но на самом деле даже хорошо обученная нейронная сеть не даст таких чистых результатов. Например, если вы вводите изображение кошки, число под меткой «Кот» может быть 0,97, число под меткой «Собака» — 0,01, а число под меткой «Прочее» — 0,02. Выходы можно интерпретировать как вероятности. Такой конкретный результат означает, что черный ящик «думает» с вероятностью 97%, что входное изображение — это изображение кота, и с небольшой вероятностью, что это либо собака, либо что-то, что он не распознает. Обратите внимание, что сумма выходных чисел равна 1.

Такая конкретная задача называется классификацией изображений; для описания изображения с наибольшей вероятностью можно использовать метку, присвоив ей имя класса (Кот, Собака, Прочее).

Что такое вход нейронной сети

Теперь вы программист и знаете, что есть числа с плавающей запятой и числа с удвоенной точностью для представления выходных данных нейронной сети.

Что для вас изображение?

Изображения — это просто массив чисел. Изображение 256\:\times\:256 с тремя каналами — это просто массив 256\:\times\:256\:\times\:3 = 196\:608 чисел. Большинство библиотек, которые вы используете для чтения изображения, считывают цветное изображение 256\:\times\:256 в непрерывный блок памяти из 196\:608 чисел.

С этими новыми знаниями мы знаем, что ввод немного сложнее. На самом деле это 196\:608 чисел. Обновим наш черный ящик, чтобы отразить нашу новую реальность.

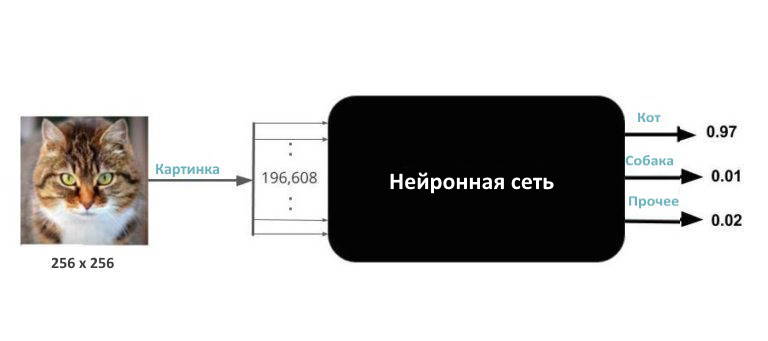
Я знаю, о чём вы подумали. Что делать с изображениями, размер которых отличается от 256\:\times\:256. Так вот, вы всегда, выполнив некоторые телодвижения, можете преобразовать любое изображение в изображение размером 256\:\times\:256.

• Неквадратное соотношение сторон: если входное изображение не квадратное, вы можете изменить размер изображения так, чтобы меньший размер составлял 256. Затем обрежьте 256\:\times\:256 пикселей от центра изображения.
• Изображение в градациях серого: если входное изображение не является цветным, вы можете создать трехканальное изображение, скопировав изображение в градациях серого в три канала.

Народ использует множество различных уловок для преобразования изображения в изображение фиксированного размера (например, 256\:\times\:256), но, поскольку я обещал, что сохраню простоту, то не буду вдаваться в подробности этих трюков. Важно отметить, что любое изображение можно преобразовать в изображение фиксированного размера, даже если мы теряем некоторую информативность при кадрировании и изменении размера изображения до этого фиксированного размера.

Что значит обучить нейронную сеть?

На черном ящике есть ручки, которые можно использовать для его «настройки». На техническом жаргоне эти ручки называются весами. Когда ручки находятся в правильном положении, нейронная сеть чаще выдает правильный выход для разных входов. Обучение нейронной сети просто означает нахождение правильных настроек ручки (или веса).

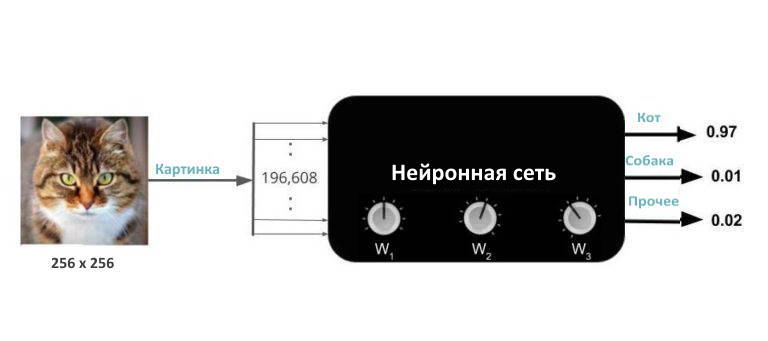
Как научить нейронную сеть?

Если бы у вас был этот волшебный черный ящик, но вы не знали правильных настроек регулятора, он был бы бесполезным.

Хорошая новость заключается в том, что вы можете найти правильные настройки регулятора, «обучив» нейронную сеть.

Обучение нейронной сети очень похоже на обучение маленького ребенка. Вы показываете ребенку мяч и говорите, что это «мяч». Когда вы проделываете это много раз с разными видами мячей, ребенок понимает, что у него форма шара, есть цвет, текстура и размер. Затем вы показываете ребенку яйцо и спрашиваете: «Что это?» он отвечает: «Мяч». Вы поправляете его и говорите, что это не мяч, а яйцо. Если этот процесс повторить несколько раз, то он станет отличать мяч от яйца.

Чтобы обучить нейронную сеть, вы показываете ей несколько тысяч примеров классов (например, Кот, Собака, Прочее), которым вы хотите её научить. Этот вид обучения называется обучением с учителем, потому что вы предоставляете нейронной сети изображение класса и явно указываете ему, что это изображение из этого класса.

Следовательно, для обучения нейронной сети нам нужны три вещи.

1. Данные для обучения: тысячи изображений каждого класса и ожидаемый результат. Например, для всех изображений кошек в этом наборе данных ожидаемый результат будет (1, 0, 0).
2. Функция стоимости: нам нужно знать, лучше ли текущая настройка, чем предыдущая. Функция стоимости суммирует ошибки, сделанные нейронной сетью по всем изображениям в обучающем наборе. Например, обычная функция стоимости называется суммой квадратов ошибок, sum of squared errors (SSE). Если ожидаемый результат для изображения Кот — (1, 0, 0), а выходы нейронной сети (0,37, 0,5, 0,13), то квадрат ошибки, сделанный нейронной сетью для этого конкретного изображения, будет (1 - 0,37)^2 + (0 - 0,5)^2 + (0 - 0,13)^2. Общая погрешность всех изображений — это просто сумма квадратов ошибок по всем изображениям. Цель обучения — найти настройки регулятора, которые минимизируют функцию стоимости.
3. Как обновить настройки регулятора: Наконец, нам нужен способ обновить настройки регулятора на основе ошибки, которую мы наблюдаем во всех обучающих изображениях.

Обучение нейронной сети с помощью одной ручки

Допустим, у нас есть тысяча изображений кошек, тысяча изображений собак и тысяча изображений случайных объектов, которые не являются кошками или собаками. Эти три тысячи изображений и есть наш обучающий набор. Если наша нейронная сеть не обучена, у неё будут некоторые случайные настройки регулятора, и когда вы введете все эти три тысячи изображений, правильным результатом будет только один из трех.

Для простоты предположим, что наша нейронная сеть имеет всего одну ручку. Поскольку у нас всего одна ручка, мы могли бы протестировать тысячи различных настроек ручки, охватывающих диапазон ожидаемых значений ручки, и найти лучшую настройку, которая минимизирует функцию стоимости. На этом наше обучение закончится.

Однако в реальных нейронных сетях ручка не единственная. Например, популярная архитектура нейронной сети VGG‑Net имеет 138 миллионов ручек!

Обучение нейронной сети с помощью нескольких регуляторов

Когда у нас была всего одна ручка, мы могли легко найти лучшую настройку, протестировав все (или очень большое количество) возможностей. Это быстро становится нереалистичным, потому что даже если бы у нас было всего три ручки, нам пришлось бы протестировать миллиарды настроек. Представьте себе количество возможностей с таким большим, как VGG‑Net. Излишне говорить, что поиск оптимальных настроек регулятора грубой силой невозможен.

К счастью, выход есть. Когда функция стоимости выпуклая (т.е. имеет форму чаши), существует принципиальный способ итеративно найти лучший вес с помощью метода, называемого градиентным спуском.

Градиентный спуск

Давайте вернемся к нашей нейронной сети с одним регулятором и предположим, что наша текущая оценка настройки регулятора (или веса) равна. Если наша функция стоимости имеет форму чаши, мы могли бы найти наклон функции стоимости и переместиться на шаг ближе к оптимальному значению регулятора. Такая процедура называется градиентным спуском, потому что мы движемся вниз (нисходя) по кривой на основе наклона (градиента). Когда вы достигнете дна чаши, градиент или наклон упадут до нуля, и на этом ваша тренировка закончится. Эти чашеобразные функции технически называются выпуклыми функциями.

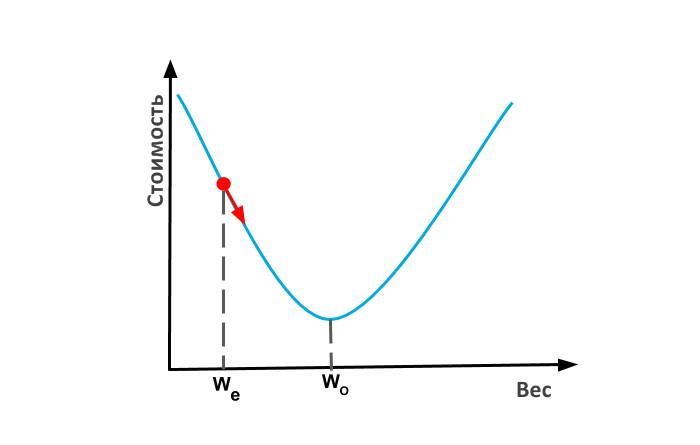
Как получить веса для первой оценки? Можете просто выбрать случайное число.

Примечание. Если вы используете популярные архитектуры нейронных сетей, такие как GoogleNet или VGG‑Net, то вместо выбора случайных начальных весов для более быстрой сходимости можете использовать вес, обученный в ImageNet.

Аналогично градиентный спуск работает и при наличии нескольких регуляторов. Например, когда есть две ручки, функция стоимости представляет собой чашу в 3D. Если мы поместим шар на любую часть этой чаши, он скатится вниз по пути максимального нисходящего наклона. Именно так работает градиентный спуск. Также обратите внимание, что если вы позволите мячу катиться вниз на полной скорости, он может пролететь мимо дна, и ему потребуется гораздо больше времени, чтобы успокоиться в нижней точке, по сравнению с шаром, который медленно катится вниз более управляемым образом. Точно так же при обучении нейронной сети мы используем параметр, называемый скоростью обучения для контроля сходимости ошибок к минимуму.

Когда у нас есть миллионы ручек (гирь), форма функции стоимости представляет собой чашу в многомерном пространстве. Несмотря на то, что такую ​​чашу невозможно визуализировать, концепция уклона и градиентного спуска работает точно так же. Следовательно, градиентный спуск позволяет нам прийти к решению, что делает проблему решаемой.

Обратное распространение

В нашем пазле осталась одна лишняя деталь. Учитывая текущие настройки регулятора, как мы узнаем наклон функции стоимости?

Во-первых, давайте вспомним, что функция стоимости и, следовательно, ее градиент зависят от разницы между истинным выходом и текущим выходом для всех изображений в обучающем наборе. Другими словами, каждое изображение в обучающем наборе участвует в окончательном вычислении градиента в зависимости от того, насколько плохо нейронная сеть работает с этими изображениями.

Алгоритм, используемый для оценки градиента функции стоимости, называется обратным распространением. Мы расскажем об обратном распространении ошибки в одном из следующих постов, и да, он действительно связан с вычислением. Вы были бы удивлены тем, что обратное распространение — это просто повторяющееся применение цепного правила, которое вы, возможно, усвоили в старших классах средней школе.

Использованная литература Neural Networks : A 30,000 Feet View for Beginners