Что такое нейронные сети прямого распространения

В этой статье мы узнаем о нейронных сетях прямого распространения, также известных как сети с глубокой прямой связью или многослойные персептроны. Они составляют основу многих важных нейронных сетей, используемых в последнее время, таких как сверточные нейронные сети^એ (широко используемые в приложениях компьютерного зрения), рекуррентные нейронные сети^એ (широко используемые для понимания естественного языка и последовательного обучения) и так далее. Мы постараемся понять важные концепции, используя интуитивно понятную игрушку и не будем вдаваясь в математику. Если вы хотите погрузиться в глубокое обучение, но не обладаете достаточным опытом в области статистики и машинного обучения, то эта статья станет идеальной отправной точкой.

Мы будем использовать сеть прямого распространения для решения задачи двоичной классификации. В машинном обучении классификация — это тип метода контролируемого обучения, в котором задача состоит в том, чтобы разделить образцы данных на заранее определенные группы с помощью функции принятия решений. Когда есть только две группы, это называется двоичной классификацией. На приведенном ниже рисунке показан пример. Точки синего цвета принадлежат одной группе (или классу), а оранжевые точки — другой. Воображаемые линии, разделяющие группы, называются границами принятия решений. Функция принятия решения извлекается из набора помеченных образцов, который называется обучающими данными, а процесс обучения функции принятия решения называется обучением.

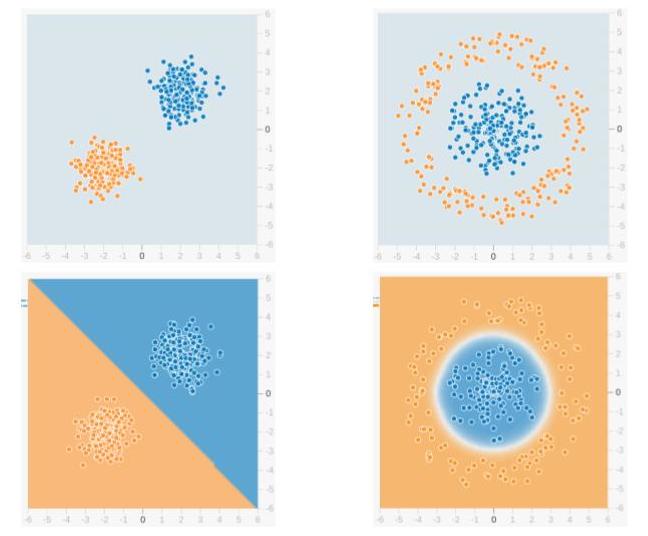
В приведенном примере верхняя строка показывает два разных распределения данных, а нижняя строка показывает границу решения. На левом изображении показан пример данных, которые можно разделить линейно. Это означает, что линейная граница (например, прямой линии) достаточно, чтобы разделить данные на группы. С другой стороны, изображение справа показывает пример данных, которые нельзя разделить линейно. Граница решения в этом случае должна быть круговой или многоугольной, как показано на рисунке.

1. Что есть нейронная сеть?

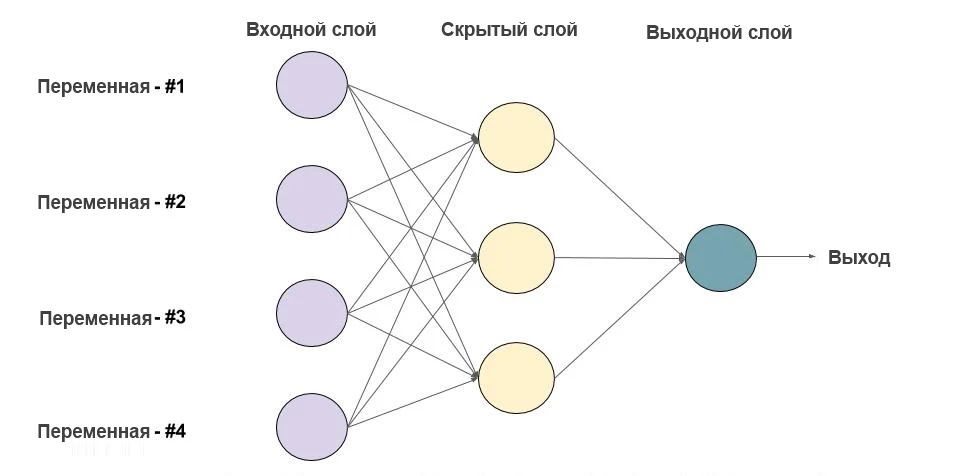
Ниже приведен пример нейронной сети прямого распространения. Это направленный ациклический граф, что означает, что в сети нет обратных связей или петель. У него есть входной слой, выходной слой и скрытый слой. Как правило, может быть несколько скрытых слоев. Каждый узел в слое — нейрон, который можно рассматривать как основной процессор нейронной сети.

1.1. Что есть нейрон?

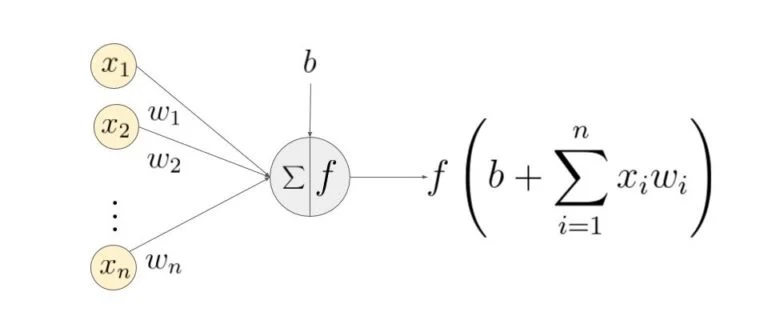
Искусственный нейрон — это основная единица нейронной сети. Принципиальная схема нейрона приведена ниже.

Как видно выше, он работает в два этапа: вычисляет взвешенную сумму своих входных данных, а затем применяет функцию активации для нормализации суммы. Функции активации могут быть линейными или нелинейными. Также, есть веса, связанные с каждым входом нейрона. Это параметры, которые сеть должна приобрести на этапе обучения.

1.2. Функции активации

Функция активации^એ используется как орган принятия решений на выходе нейрона. Нейрон изучает линейные или нелинейные границы принятия решений на основе функции активации. Он также оказывает нормализующее влияние на выход нейронов, что предотвращает выход нейронов после нескольких слоев, чтобы стать очень большим, за счет каскадного эффекта. Есть три наиболее часто используемых функции активации.

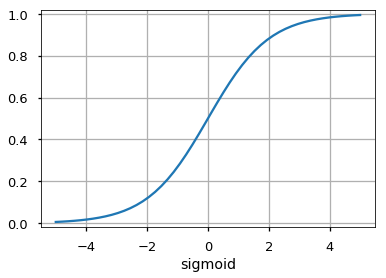
Сигмоида^એ
Он отображает входные данные (ось x) на значения от 0 до 1.

Tanh
Похожа на сигмовидную функцию, но отображает входные данные в значения от -1 до 1.

Rectified Linear Unit (ReLU)
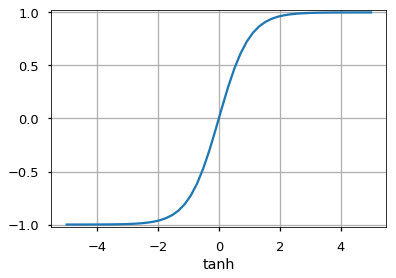
Он позволяет проходить через него только положительным значениям. Отрицательные значения отображаются на ноль.

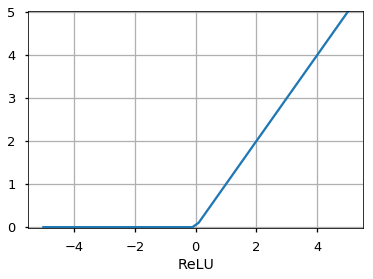
Функция активации^એ может быть другой, например, функция Unit Step, leaky ReLU, Noisy ReLU, Exponential LU и т.д., которые имеют свои плюсы и минусы.

1.3. Входной слой

Это первый слой нейронной сети. Он используется для передачи и приёма входных данных или функций в сеть.

1.4. Выходной слой

Это слой, который выдает прогнозы. Функция активации, используемая на этом уровне, различается для разных задач. Для задачи двоичной классификации мы хотим, чтобы на выходе было либо 0, либо 1. Таким образом, используется сигмовидная функция активации. Для задачи мультиклассовой классификации используется Softmax^એ (воспринимайте это как обобщение сигмоида на несколько классов). Для задачи регрессии, когда результат не является предопределенной категорией, мы можем просто использовать линейную единицу.

1.5. Скрытый слой

Сеть прямого распространения применяет к входу ряд функций. Имея несколько скрытых слоев, мы можем вычислять сложные функции, каскадируя более простые функции. Предположим, мы хотим вычислить седьмую степень числа, но хотим, чтобы вещи были простыми (поскольку их легко понять и реализовать). Вы можете использовать более простые степени, такие как квадрат и куб, для вычисления функций более высокого порядка. Точно так же вы можете вычислять очень сложные функции с помощью этого каскадного эффекта. Наиболее широко используемый скрытый блок — это тот, где функция активации^એ использует выпрямленный линейный блок (ReLU). Выбор скрытых слоёв — очень активная область исследований в машинном обучении. Тип скрытого слоя отличает разные типы нейронных сетей, такие как CNN^એ, RNN^એ и т.д. Количество скрытых слоев называется глубиной нейронной сети. Вы можете задать вопрос: сколько слоев в сети делают ее глубокой? На это нет правильного ответа. В общем случае, более глубокие сети могут научиться более сложным функциям.

1.6. Как сеть учится?

Обучающие образцы передаются по сети, и выходные данные, полученные от сети, сравниваются с фактическими выходными данными. Эта ошибка используется для изменения веса нейронов таким образом, чтобы ошибка постепенно уменьшалась. Это делается с помощью алгоритма обратного распространения ошибки, также называемого обратным распространением. Итеративная передача пакетов данных по сети и обновление весов для уменьшения ошибки называется стохастический градиентный спуск^એ (SGD). Величина, на которую изменяются веса, определяется параметром, называемым «Скорость обучения». Подробности SGD и backprop будут описаны в отдельном посте.

2.Зачем использовать скрытые слои?

Чтобы понять значение скрытых слоев, мы попытаемся решить проблему двоичной классификации без скрытых слоев. Для этого мы будем использовать интерактивную платформу от Google, plays.tensorflow.org, которая представляет собой веб-приложение, где вы можете создавать простые нейронные сети с прямой связью и видеть эффекты обучения в реальном времени. Вы можете поиграть, изменив количество скрытых слоев, количество нейронов в скрытом слое, тип функции активации, тип данных, скорость обучения, параметры регуляризации и т.д. Выше приведен снимок экрана веб-страницы.

На приведенной выше странице вы можете выбрать данные и нажать кнопку воспроизведения, чтобы начать обучение.
Он покажет вам изученную границу решения и кривые потерь в правом верхнем углу.

2.1. Без скрытого слоя

Нам нужна сеть без скрытого слоя, который я создал по этой ссылке. Здесь нет скрытых слоев, поэтому он становится простым нейроном, способным изучать линейную границу принятия решения. Мы можем выбрать тип данных в верхнем левом углу. В случае линейно разделяемых данных (3-й тип), он сможет получить (когда вы нажмете кнопку воспроизведения) линейную границу, как показано ниже.

Однако, если вы выберете первые данные, вы не сможете для них узнать границу кругового решения.

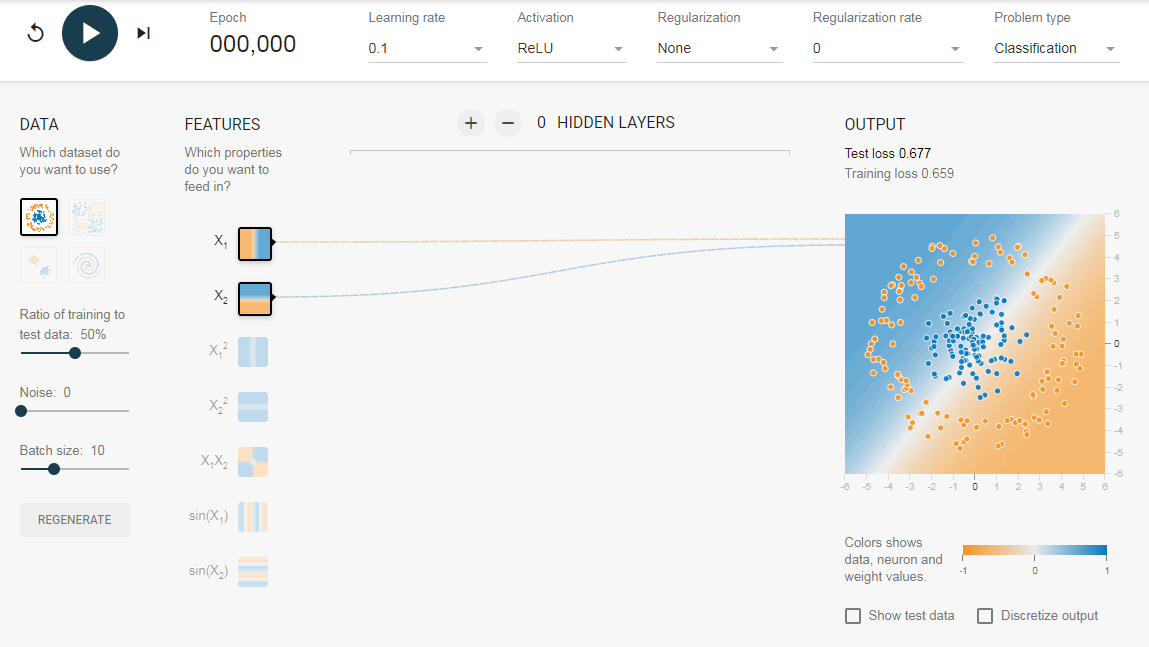
Поскольку данные находятся в круговой области, можно сказать, что использование квадратов значений функций в качестве входных данных может помочь. Оказывается, после обучения нейрон сможет найти круговую границу принятия решения.

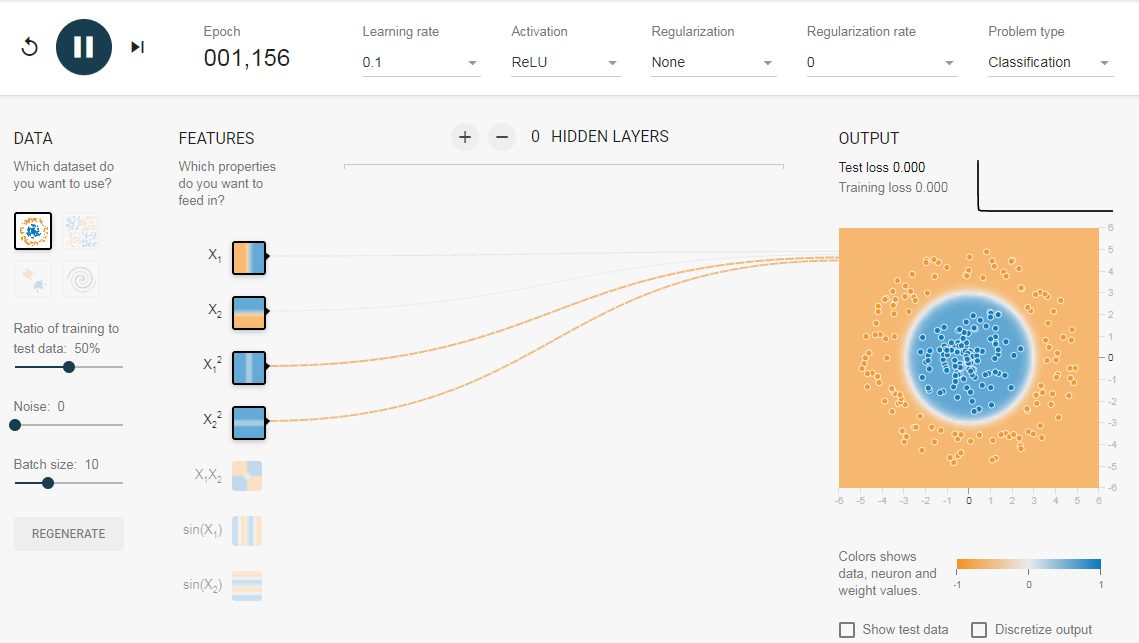
Теперь, если вы выберете 2-е данные, та же конфигурация не сможет узнать соответствующую границу решения.

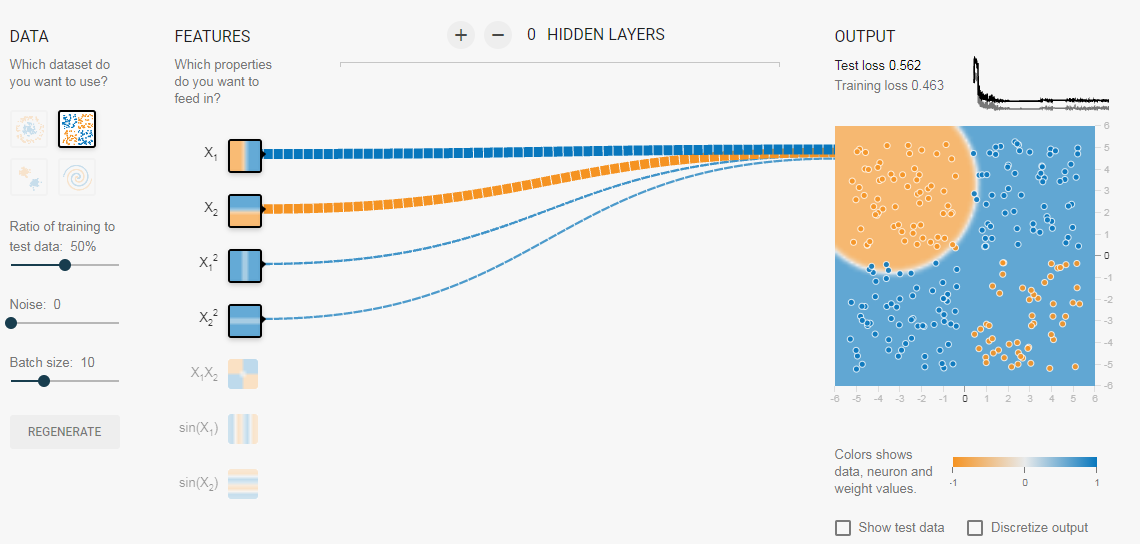
Опять же интуитивно кажется, что граница решения — это коническое сечение (например, парабола или гипербола). Итак, если мы включим продукт функции (например, X_1 X_2), нейрон сможет узнать желаемую границу принятия решения.

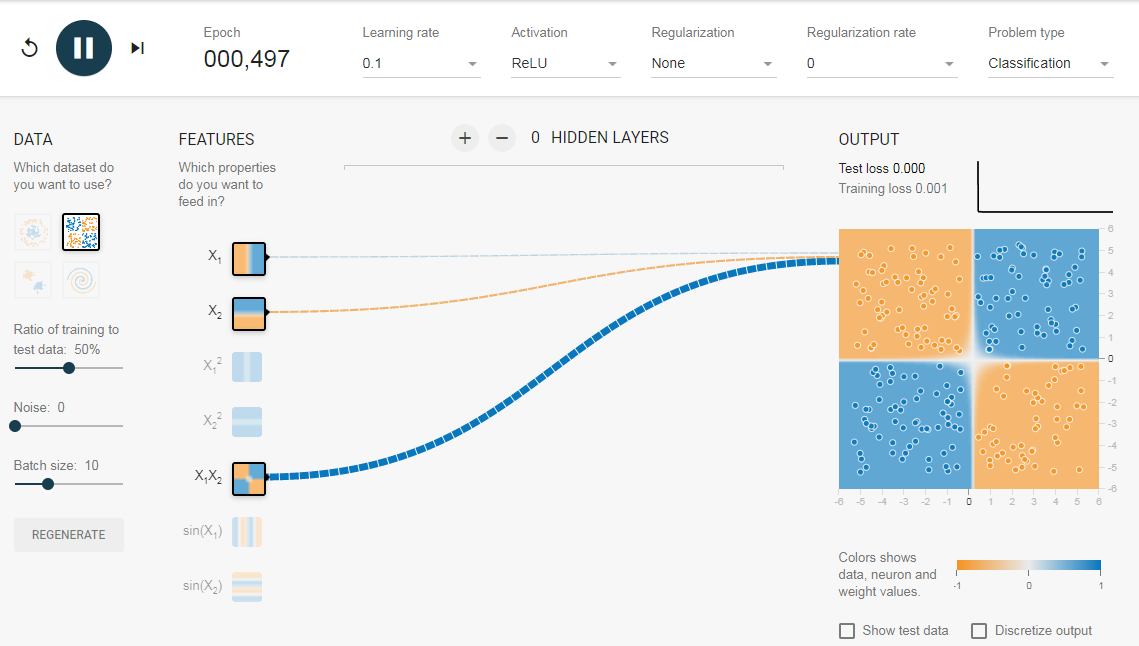
Описанные эксперименты показали:

• Используя один нейрон, мы можем узнать только линейную границу решения.
• Нам пришлось придумать преобразования функций (например, квадрат функций или продукт функций) путем визуализации данных. Этот шаг может быть сложным для данных, которые нелегко визуализировать.

2.2. Добавление скрытого слоя

Добавив скрытый слой, как показано в этой ссылке, мы можем избавиться от этой функции проектирования и получить единую сеть, которая может изучить все три границы принятия решений. Нейронная сеть с одним скрытым слоем с нелинейными функциями активации считается универсальным аппроксиматором функций, теорема Цыбенко^એ (т.е. способной к обучению любой функции). Однако количество единиц в скрытом слое не фиксировано. Результат добавления скрытого слоя всего с 3 нейронами показан ниже:

3. Регуляризация

Как мы видели в предыдущем разделе, многослойная сеть может изучать нелинейные границы принятия решений. Однако, если в данных есть шум (что часто бывает), сеть может попытаться изучить нелинейность, вносимую шумом, пытаясь подогнать зашумленные выборки. В таких случаях зашумленные образцы следует рассматривать как выбросы. В этой ссылке я добавил немного шума к линейно разделяемым данным. Также, чтобы продемонстрировать идею, я увеличил количество скрытых нейронов.

На приведенном выше рисунке можно увидеть, что граница принятия решения очень старается приспособить зашумленные выборки, чтобы уменьшить ошибку. Но, как видите, это ошибочно из-за шумных сэмплов. Другими словами, сеть будет неустойчивой при наличии шума. Это явление называется переобучением. В таких случаях, ошибка обучающих данных может уменьшиться, но сеть плохо работает с невидимыми данными. Это видно по кривым потерь в правом верхнем углу.

Потери в обучении уменьшаются, но потери в тестах увеличиваются. Также, можно видеть, что некоторые веса стали очень большими (очень толстые соединения или вы можете увидеть веса, если наведете курсор на соединения). Это можно исправить, наложив некоторые ограничения на значения весов (например, не позволяя весам становиться очень высокими). Это называется регуляризацией. Мы накладываем ограничения на остальные параметры сети. В некотором смысле мы не полностью доверяем обучающим данным и хотим, чтобы сеть усвоила «хорошие» границы принятия решений. Я добавил регуляризацию L2 в приведенную выше конфигурацию по этой ссылке, и результат показан ниже.

После включения регуляризации L2 граница принятия решения, изученная сетью, становится более гладкой и аналогичной случаю, когда не было шума. Эффект регуляризации также можно увидеть из кривых потерь и значений весов.

В следующем посте, если он случится мы узнаем, как реализовать нейронную сеть прямого распространения в Keras для решения нескольких проблема классификации и узнайте ещё больше о сетях прямого распространения.

Использованы материалы Understanding Feedforward Neural Networks