Парадокс дня рождения формулируется просто: если в комнате 23 человека, то с вероятностью 50% у двоих из них день рождения совпадает.
А не много ли?
Я не собираюсь углубляться в математику, но причина, по которой это кажется таким запутанным, заключается в том, что изначально, чтобы найти совпадение мы думаем о сравнении только собственного дня рождения с 22 другими. Это оставляет нам только 22 пары дней рождения для проверки. На самом деле, чтобы найти совпадение нам нужно сравнить день рождения каждого с каждым из 22 других. Первый человек сравнивает свой день рождения с 22 другими, второй сравнивает свой день рождения с 21-м (минус первый, потому что они уже сравнивались), третий сравнивает с 20-ю и так далее. В конце концев для поиска совпадений нам надо проверить 253 пары дней рождения.
Вот так! И в этой логике есть смысл. Но все равно, как часто бывает с подобными невероятными математическими фактами, ЕСТЬ СОМНЕНИЯ, что всё это не правда, не так ли?
Хотя собрать несколько групп из 23 незнакомцев и потребовать, чтобы все они поделились датой своего рождения, является самым надежным вариантом, но на этом пути мы поимеем некоторые логистические и этические проблемы. По этой причине я решил использовать Python и провёл 250 испытаний, в которых выбрал 23 случайных числа от 1 до 365 и проверил, совпадают ли какие-либо из 23 и посчитал эти экземпляры successes. Далее посчитал их вероятность относительно общего количества испытаний:
import pandas as pd # для датафрейма
import random # будем генерить случайные числа
import plotly.express as px # будем показывать интерактивные графики
results, trials = [], []
successes = 0
for i in range(1, 250):
test = [random.randint(1, 365) for i in range(23)]
if len(test) != len(set(test)): # День рождения
successes += 1
results.append(successes/i)
else:
results.append(successes/i)
trials.append(i)
Выгружаем результаты в DataFrame Pandas и покажем их на графике:
bday_df = pd.DataFrame(data={"Trials": trials, "Results": results})
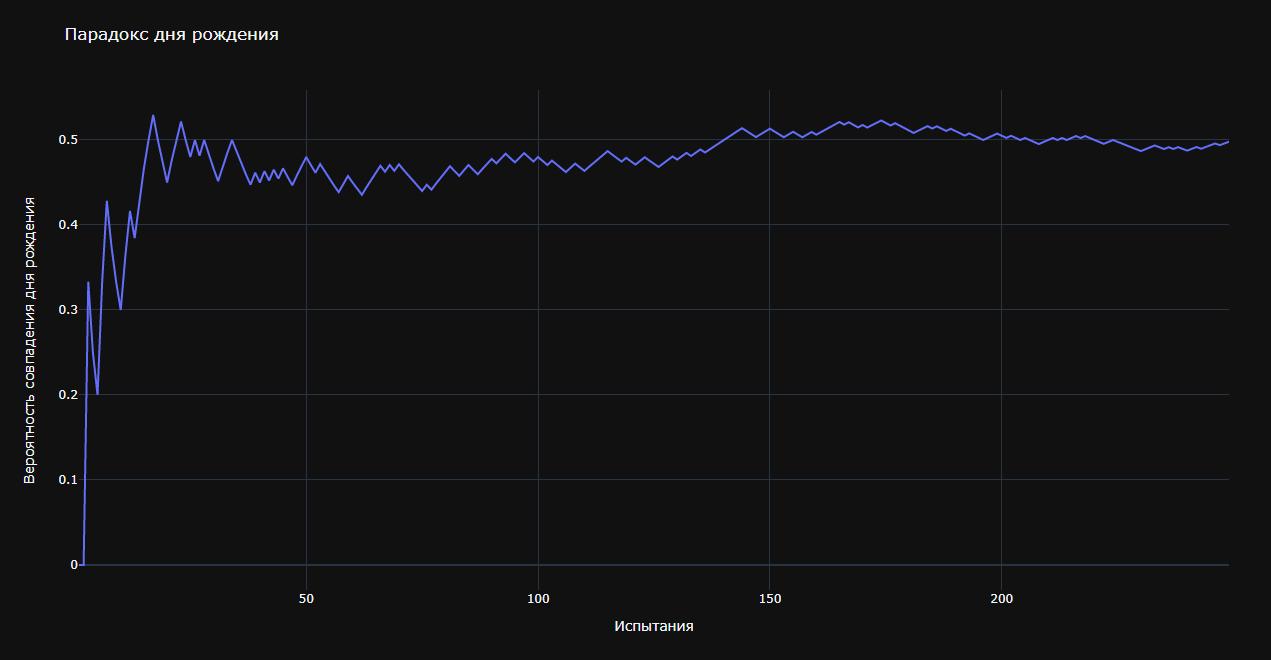
fig = px.line(bday_df, x = "Trials", y = "Results", labels={"Trials": "Испытания", "Results": "Вероятность совпадения дня рождения"},
title="Парадокс дня рождения", template='plotly_dark')
fig.show()
Как вы можете убедиться, хотя вначале наблюдаются некоторые колебания, к отметке 150 испытаний вероятность того, что два из 23 человек смогут вместе праздновать день рождения, составила около 50%. Если мы позволим поработать своему скрипту, скажем, еще 10 000 испытаний, то график полностью выровняется на уровне 50%.
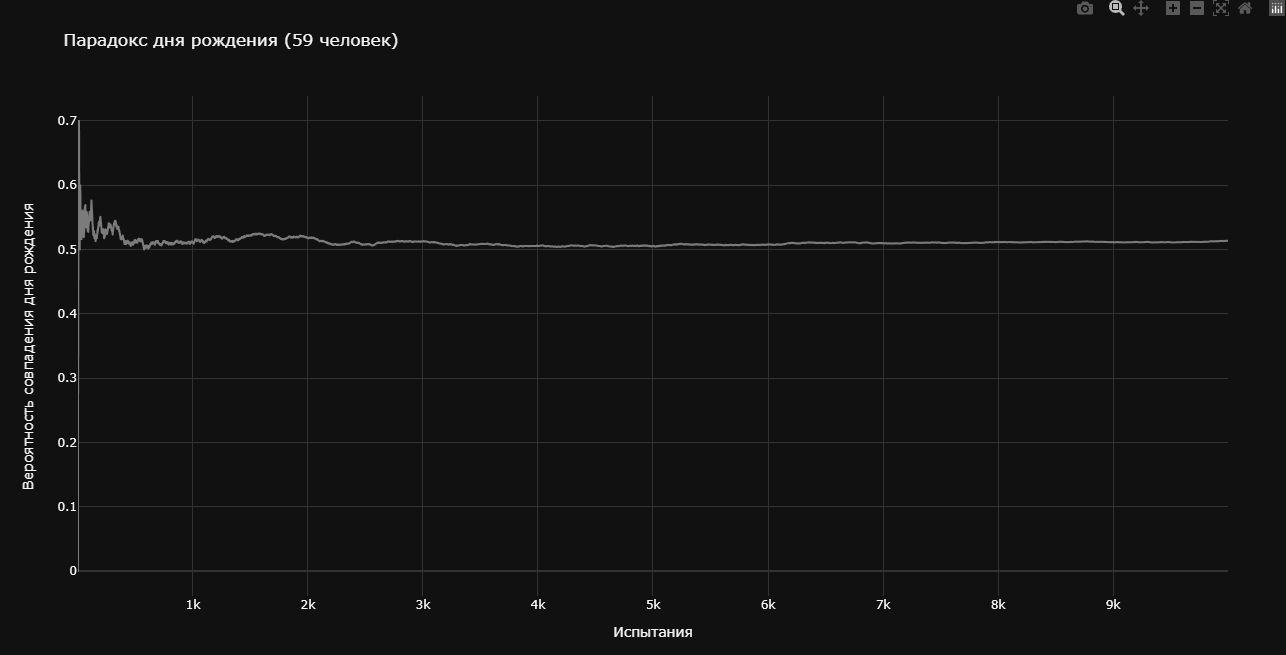
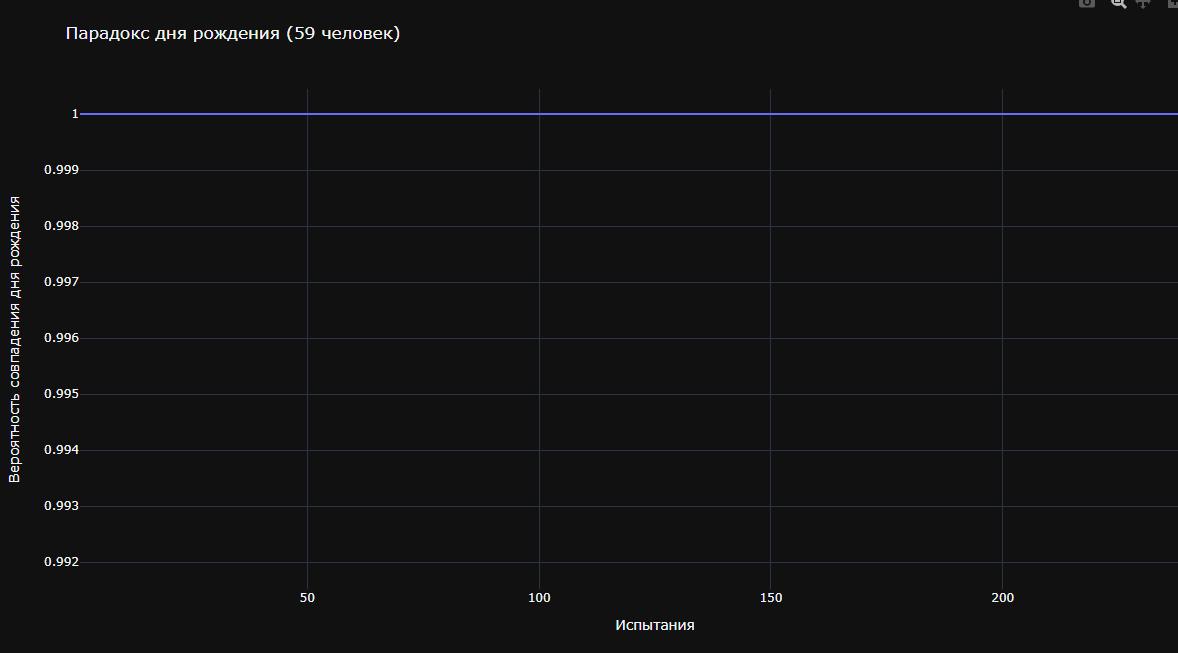
Парадокс дня рождения также утверждает, что если 59 человек находятся в одной комнате, то вероятность того, что у двоих из них день рождения совпадает, практически гарантирована на уровне 99%.
Для 59 человек график становится прямой линией. В этом можно убедиться, наведя курсор на точку графика в браузере.
Диаграмма вероятности парадокса дня рождения показана с кодом и графиками ниже:
import pandas as pd
import random
import plotly.express as px
ppl_in_room, probability = [], []
for i in range(1, 75):
probability.append(round(1 - (364/365)**((i*(i-1))/2), 4))
ppl_in_room.append(i)
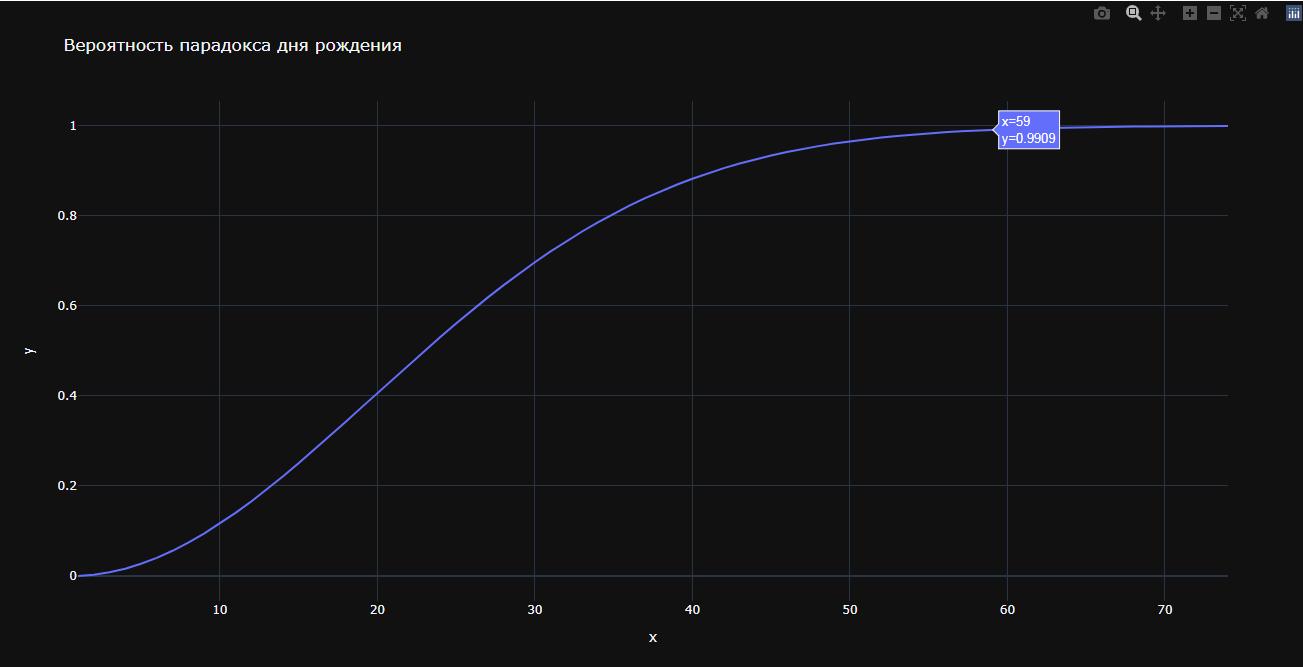
fig = px.line(x = ppl_in_room, y = probability, title='Вероятность парадокса дня рождения', template='plotly_dark')
fig.show()
Прямо при x = 23 линия пересекает порог вероятности 0,50. К x = 59 кривая сглаживается по мере приближения к 1.0; он остается таким до x = 366, после чего вероятность становится равной 1.0.
Ну вот и все.
В следующий раз, когда вместе с вами в одной комнате будет ещё 22 человека, можете быть уверены, что по крайней мере у двоих из них дни рождения совпадают. А если подойдут еще 39 человек в то-же место, то можно смело заключать и выигрывать пари, что по крайней мере двое из них родились в один день.
Было кому-нибудь интересно? Будет ли кому-нибудь от этого польза? — Не знаю. Но не всегда же быть серьёзным.
Требуется регистрация для доступа к контенту. Регистрация, если Вы уже зарегистрированы — подключитесь
![]() Парадокс дня рождения, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Парадокс дня рождения, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Респект и уважуха