Камера является неотъемлемой частью многих автоматизированных систем, например, в робототехнике, в наблюдениях и исследовании космоса, в социальных сетях, промышленной автоматизации и даже в индустрии развлечений.
Для эффективного использования камер во многих приложениях особенно важно знать их характеристики.
Здесь вы узнаете шаги калибровки камеры и поймете их значение. Кроме того, на примере шахматной доски мы поделимся кодом Python для калибровки.
Поехали…
Что такое калибровка камеры?
Калибровкаએ — это процесс оценки параметров камеры.
Это значит, что у нас есть полная информация (технические характеристики или расчетные коэффициенты) о камере, необходимые для определения точной взаимосвязи между 3D‑точкой в реальном мире и соответствующим 2D‑изображением, проекцией (каждым пикселем) на изображении, снятом откалиброванной камерой.
Обычно для этого необходимо получить два вида параметров:
- Внутренние параметры системы камера/объектив. Например, фокусное расстояние, оптический центр и коэффициенты радиального искажения объектива.
- Внешние параметры, связанные с ориентацией (поворотом и смещением) камеры относительно некоторой мировой системы координат.
На рисунке ниже для искажения изображения были использованы параметры объектива, оцененные при геометрической калибровке.

Калибровка камеры с использованием OpenCV
Для понимания процесса калибровки, нам сначала необходимо понять геометрию формирования изображения. Как показано в предыдущей публикации (желательно её прочитать, нажав на ссылку), чтобы найти проекцию 3D‑точки на плоскость изображения, сначала надо перевести точку (X_w, Y_w, Z_w) из мировой системы координат в систему координат камеры с учётом внешних параметров (Вращение R и Смещение t).
Далее, используя внутренние параметры камеры, мы проецируем точку на плоскость изображения. Уравнения, которые связывают трехмерную точку (X_w, Y_w, Z_w) в мировых координатах с её проекцией в координатах изображения (u, v), записаны ниже:
\begin{bmatrix}u'\\v'\\w'\end{bmatrix} = \mathbf{P} \begin{bmatrix} X_w\\ Y_w\\ Z_w \\ 1 \end{bmatrix}
u = \frac{u'}{w'} \\ v = \frac{v'}{w'}
Где \mathbf{P} — матрица проекции размером 3 × 4, состоящая из двух частей: 1) внутренней матрицы \mathbf{K}, которая содержит внутренние параметры и 2) внешнюю матрицу ([\mathbf{R}\mid\mathbf{t}]), которая является комбинацией матрицы вращения размером 3 × 3 и \mathbf{R} и вектора преобразования 3 × 1 \mathbf{t}.
\mathbf{P} = \mathbf{K} * [\mathbf{R} \mid \mathbf{t}]
Как упоминалось в предыдущем посте, внутренняя матрица \mathbf{K} является верхней треугольной.
\mathbf{K} = \begin{bmatrix}f_x&\gamma&c_x\\0&f_y&c_y&\\0&0&1\end{bmatrix}
где, f_x, f_y — фокусные расстояния x и y (да, они обычно одинаковы).
c_x, c_y — координаты x и y оптического центра в плоскости изображения. Использование центра изображения обычно является достаточно хорошим приближением.
\gamma — это перекос между осями. Обычно это 1.
Цель калибровки камеры
Цель процесса калибровки — найти матрицу \mathbf{K} размером 3 × 3, матрицу вращения 3 × 3 \mathbf{R} и вектор перевода \mathbf{t}, используя набор известных трехмерных точек (X_w, Y_w, Z_w) и соответствующие им координаты изображения (u, v). Когда мы получаем значения внутренних и внешних параметров, камера считается откалиброванной.
Таким образом, алгоритм калибровки камеры имеет следующие входы и выходы:
- Входные данные: коллекция изображений с точками, чьи координаты 2D-изображения и 3D-мировые координаты известны.
- Выходы: собственная матрица камеры 3 × 3, поворот и перемещение каждого изображения.
Примечание. В OpenCV встроенная матрица камеры не имеет параметра перекоса. Таким образом, матрица имеет вид
\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}
Методы калибровки камеры
Ниже перечислены основные методы калибровки камеры:
- Калибровка по шаблону: Когда мы полностью контролируем процесс формирования изображения, лучший способ выполнить калибровку — это сделать несколько изображений объекта или шаблона известных размеров с разных точек зрения. Метод шахматной доски, который мы изучим в этом посте, относится именно к этой категории. Вместо рисунка шахматной доски можно использовать круглые узоры известных размеров.
- Геометрические примитивы. Иногда в сцене присутствуют другие геометрические примитивы, например прямые линии и точки пересечений, которые также можно использовать для калибровки.
- На основе глубокого машинного обучения: Когда у нас очень ограничены возможности управления настройками изображения (например, у нас есть единственное изображение сцены), при этом всё еще возможно получить информацию для калибровки камеры, используя Метод глубокого машинного обучения.
Калибровка камеры — шаг за шагом
Процесс калибровки объясняется блок-схемой, приведенной ниже.
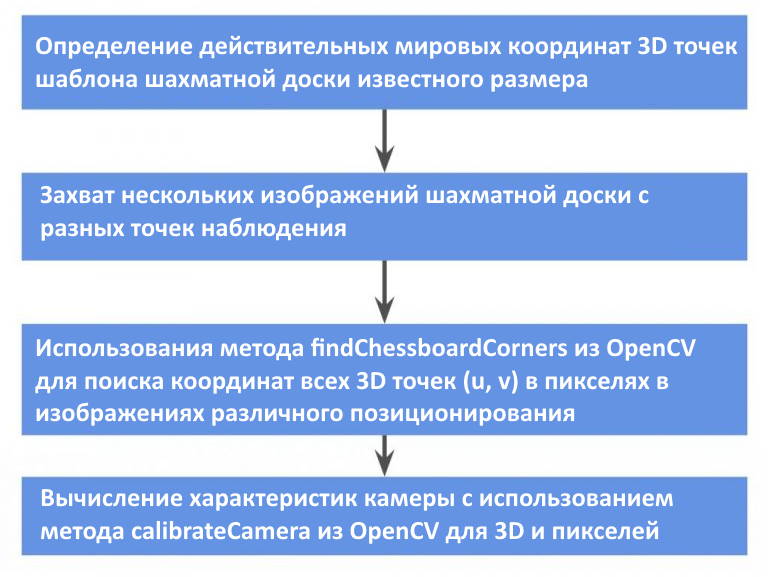
Шаг 1: Определение действительных мировых координат 3D точек шаблона шахматной доски известного размера

Наши 3D точки — это углы клеток шахматной доски. Любой угол доски может быть выбран в качестве начала мировой системы координат. Оси X_w и Y_w расположены вдоль стены, а ось Z_w перпендикулярна стене. Поэтому все точки на шахматной доске находятся на плоскости XY (т.е. Z_w = 0).
Для трехмерных точек мы фотографируем шахматную доску с известными размерами при разных ориентациях. Мировая координата связана с шахматной доской. Поскольку все угловые точки лежат на плоскости, мы можем произвольно выбрать Z_w для каждой точки равным 0. Поскольку точки на шахматной доске расположены на равном расстоянии, координаты (X_w, Y_w) каждой 3D точки можно легко определить, взяв одну точку за начало отсчета (0, 0) и определив оставшуюся точку относительно этой точки отсчета.
Почему шахматная доска так широко используется в калибровке?
Клетки шахматной доски легко различимы на изображении и их легко обнаружить. Более того, углы клеток шахматной доски идеально подходят для их локализации, поскольку имеют резкие градиенты в двух направлениях. Кроме того, углы находятся на пересечении линий шахматной доски. Все эти факторы определяют надежность поиска углов клеток, расположенных в шахматном порядке.

Шаг 2: Захват нескольких изображений шахматной доски с разных точек наблюдения

Затем, не изменяя местоположение нашей шахматной доски, мы делаем несколько снимков, смещая камеру.
Можно зафиксировать камеру, а смещать шахматную доску. С точки зрения математики это одно и то-же.
Шаг 3: Вычисление 2D координат клеток шахматной доски в пикселях
Теперь у нас есть несколько изображений шахматной доски. Мы знаем 3D координаты точек шахматной доске. Последнее, что нам нужно, это координаты углов клеток шахматной доски на изображениях в пикселях.
3.1 Поиск углов шахматной доски
В OpenCV есть встроенная функция findChessboardCorners, которая ищет шахматную доску и возвращает координаты углов. Посмотрим, как она используется в кода на Python
retval, corners = cv2.findChessboardCorners(image, patternSize, flags)
Здесь,
- image — Исходный вид шахматной доски. Должен быть цветным или 8-битным изображением в оттенках.
- patternSize — Количество клеток шахматной доски по вертикали и горизонтали (patternSize = cvSize (points_per_row, points_per_colum) = cvSize(columns,rows)).
- corners — Output array of detected corners.
- flags — Различные флаги. О них надо побеспокоится только тогда, когда что-то не работает. Оставьте значение по умолчанию.
Возвращаемое значение функции true или false в зависимости от того, был обнаружен шаблон или нет.
3.2 Уточнение координат клеток шахматной доски
Хорошая калибровка — это точность. Чтобы получить хорошие результаты, важно получить координаты клеток с субпиксельной точностью.
Функция OpenCV cornerSubPix берет клетки исходного изображения и ищет лучшее местоположение углов клеток, расположенных по соседству. По своей сути алгоритм является итерационным и поэтому нам необходимо указать критерии завершения (например, количество итераций и/или точность).
Python
cv2.cornerSubPix(image, corners, winSize, zeroZone, criteria)
Здесь,
- image — Исходное изображение.
- corners — Начальные координаты входных углов и уточненные координаты, которые передаются в вызывающую функцию.
- winSize — Половина длины стороны окна поиска.
- zeroZone — Половина размера мертвой области в середине зоны поиска, по которой суммирование в приведенной ниже формуле не выполняется. Это иногда используется, чтобы избежать возможных особенностей матрицы автокорреляции. Значение (-1, -1) указывает, что такого размера нет.
- criteria — Критерии прекращения итерационного процесса уточнения угла. То есть процесс уточнения координат угла прекращается либо после выполнения заданного количества итераций
criteria.maxcount, либо при достижении заданной точностиcriteria.epsilonмежду итерациями.
Step 4: Калибровка камеры
Последний шаг калибровки состоит в том, чтобы передать 3D-точки в мировых координатах и их 2D-положения на всех изображениях в метод calibrateCamera OpenCV. Реализация основана на статье «A Flexible New Technique for Camera
Calibration» Чжэнъю Чжан. Математика немного сложна и требует знания линейной алгебры.
Давайте посмотрим на синтаксис calibrateCamera:
retval, cameraMatrix, distCoeffs, rvecs, tvecs = cv2.calibrateCamera(objectPoints, imagePoints, imageSize)
Здесь,
- objectPoints — Вектор векторов 3D точек.
Внешний вектор содержит столько же элементов, сколько число представлений образца.
- imagePoints — Вектор векторов 2D точек.
- imageSize — Размер изображения
- cameraMatrix — Внутренняя матрица камеры
- distCoeffs — Коэффициенты искажения объектива. Эти коэффициенты будут объяснены в будущем посте.
- rvecs — Вращение указано как вектор 3 × 1. Направление вектора задает ось вращения, а величина вектора — угол поворота.
- tvecs — 3×1 вектор смещения.
Код для калибровки камеры
Код для калибровки камеры приведен ниже. Однако загрузить все изображения и код намного проще, посетив Github.
Скрипт Python для калибровки камер
Пожалуйста, внимательно прочитайте комментарии, объясняющие каждыйшаг
#!/usr/bin/env python
import cv2
import numpy as np
import os
import glob
# Определение размеров шахматной доски
CHECKERBOARD = (6,9)
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# Создание вектора для хранения векторов трехмерных точек для каждого изображения шахматной доски
objpoints = []
# Создание вектора для хранения векторов 2D точек для каждого изображения шахматной доски
imgpoints = []
# Определение мировых координат для 3D точек
objp = np.zeros((1, CHECKERBOARD[0] * CHECKERBOARD[1], 3), np.float32)
objp[0,:,:2] = np.mgrid[0:CHECKERBOARD[0], 0:CHECKERBOARD[1]].T.reshape(-1, 2)
prev_img_shape = None
# Извлечение пути отдельного изображения, хранящегося в данном каталоге
images = glob.glob('./images/*.jpg')
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Найти углы шахматной доски
# Если на изображении найдено нужное количество углов, тогда ret = true
ret, corners = cv2.findChessboardCorners(gray, CHECKERBOARD, cv2.CALIB_CB_ADAPTIVE_THRESH + cv2.CALIB_CB_FAST_CHECK + cv2.CALIB_CB_NORMALIZE_IMAGE)
"""
Если желаемый номер угла обнаружен,
уточняем координаты пикселей и отображаем
их на изображениях шахматной доски
"""
if ret == True:
objpoints.append(objp)
# уточнение координат пикселей для заданных 2d точек.
corners2 = cv2.cornerSubPix(gray, corners, (11,11),(-1,-1), criteria)
imgpoints.append(corners2)
# Нарисовать и отобразить углы
img = cv2.drawChessboardCorners(img, CHECKERBOARD, corners2, ret)
cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()
h,w = img.shape[:2]
"""
Выполнение калибровки камеры с помощью
Передача значения известных трехмерных точек (объектов)
и соответствующие пиксельные координаты
обнаруженные углы (imgpoints)
"""
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
print("Camera matrix : \n")
print(mtx)
print("dist : \n")
print(dist)
print("rvecs : \n")
print(rvecs)
print("tvecs : \n")
print(tvecs)
По мотивам:
![]() Калибровка камеры с использованием с OpenCV, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Калибровка камеры с использованием с OpenCV, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Респект и уважуха


