Введение в эпиполярную геометрию и стереозрение

Вы когда-нибудь задумывались, почему можно испытать этот чудесный 3D-эффект, когда смотрите фильм в этих специальных 3D-очках? Или почему сложно поймать мяч для крикета с одним закрытым глазом? Все это относится к стереоскопическому зрению, то есть нашей способности воспринимать глубину обоими глазами. Этот пост использует OpenCV и стереозрение для вычисления глубины изображения. Код предоставляется на Python.

Крутизна этой GIF-ки заключается в том, что помимо обнаружения различных объектов компьютер может определять, как далеко они находятся. Значит, он может воспринимать глубину! Для этого видео использовалась стереокамера OAK-D (OpenCV AI Kit-Depth) и компьютер может воспринимать глубину. Что такое настройка стереокамеры? Как мы можем использовать её, чтобы придать компьютеру ощущение глубины? Это как-то связано со стереоскопическим зрением?

Здесь я попытаюсь ответить на эти вопросы, используя фундаментальные концепции, связанные с эпиполярной геометрией и стереозрением.

Большинство теоретических объяснений этой статьи основано на книге Richard Hartley and Andrew Zisserman. 2003. Multiple View Geometry in Computer Vision [1] (Ричарда Хартли и Эндрю Зиссермана «Геометрия с множеством представлений в компьютерном зрении»). Это очень известный и стандартный учебник для понимания различных фундаментальных концепций компьютерного зрения.

Итак, давайте начнем и поможем своему компьютеру ощутить глубину!

Сколько нужно изображений для расчета глубины?>

Когда мы захватываем (проецируем) трехмерный объект на изображение, мы проецируем его из трехмерного пространства в двухмерное (плоское) проективное пространство. Это называется плоской проекцией. Проблема в том, что из-за этой плоской проекции мы теряем информацию о глубине.

Как восстановить глубину? Можно ли рассчитать глубину сцены, используя одно изображение? Посмотрим на простой пример.

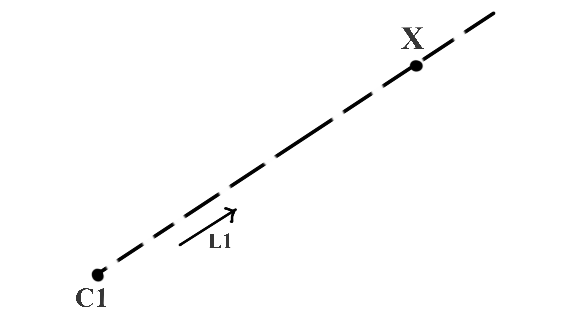
На рисунке 1 C1 и X являются точками в трехмерном пространстве, а единичный вектор L1 дает направление луча от C1 до X. Теперь можем ли мы найти X, если мы знаем значения точки C1 и вектора направления L1? Математически это просто означает найти X в уравнении

X = C1 + k(L1)

Теперь, поскольку значение k неизвестно, мы не можем найти уникальное значение X.

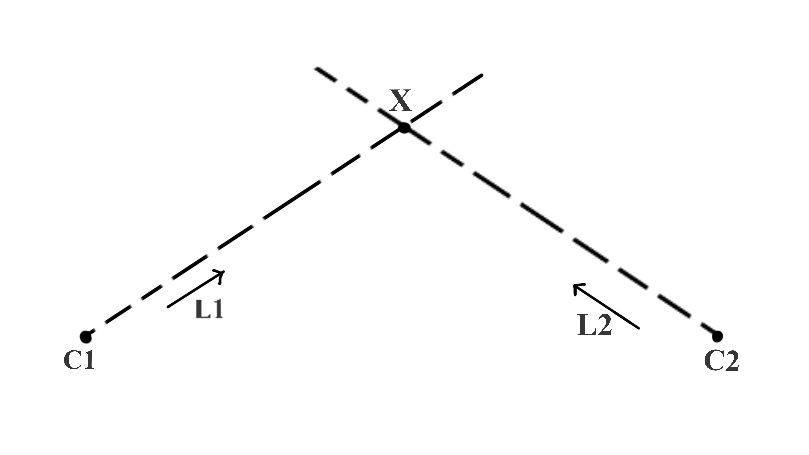
На рисунке 2 у нас есть дополнительная точка C2, а L2 — вектор направления луча от C2 до X. Теперь можем ли мы найти уникальное значение для X, если C2 и L2 также нам известны?

Да! Поскольку лучи, исходящие из C1 и C2, явно пересекаются в единственной точке — самой точке X. Это называется триангуляцией. Мы говорим, что мы триангулировали точку X.

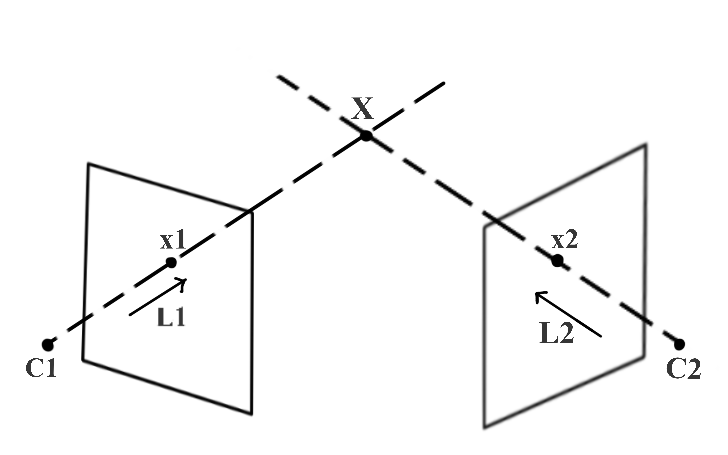
На рисунке 3 показано, как можно использовать триангуляцию для вычисления глубины точки (X) при захвате (проецировании) в двух разных видах (изображениях). На этом рисунке C1 и C2 — известные трехмерные положения левой и правой камер соответственно. x1 — это изображение трехмерной точки X, снятое левой камерой, а x2 — изображение X, снятое правой камерой. x1 и x2 называются соответствующими точками, потому что они являются проекцией одной и той же трехмерной точки. Мы используем x1 и C1, чтобы найти L1, и x2 и C2, чтобы найти L2. Следовательно, мы можем использовать триангуляцию для нахождения X точно так же, как на рисунке 2.

Из приведенного выше примера понятно, что для триангуляции трехмерной точки с использованием двух изображений, снятых с разных ракурсов, необходимо знать:

• Расположение камер — С1 и С2.
• Точечное соответствие — x1 и x2.

Великолепно! Теперь ясно, что для определения глубины нам нужно более одного изображения. Привет! но это была всего лишь одна трехмерная точка, которую мы пытались вычислить. Как рассчитать трехмерную структуру реальной сцены, захватив ее с двух разных точек зрения? Очевидный ответ — повторить описанный выше процесс для всех трехмерных точек, захваченных в обоих видах. Давайте подробнее рассмотрим практические проблемы. Время на проверку реальности!

Практическое и теоретическое понимание геометрии с двух точек зрения

На рисунке 4 показаны два изображения, запечатлевшие реальную сцену с разных точек зрения. Чтобы рассчитать трехмерную структуру, мы пытаемся найти два ключевых требования, упомянутых ранее:

1. Положение камер в реальной системе координат (C1 и C2).Мы упрощаем эту задачу, вычисляя трехмерные точки, принимая одно из положений камеры (C1 или C2) в качестве начала координат. Мы находим это путем калибровки системы двух представлений с использованием известного шаблона калибровки. Этот процесс называется стереокалибровкой.
2. Соответствие точек (x1 и x2) для каждой трехмерной точки (X) в сцене, которую нужно вычислить.Мы обсудим различные улучшения для вычисления соответствия точек и, наконец, поймем, как эпиполярная геометрия может помочь нам упростить задачу.

Обратите внимание, что калибровка стереокамеры полезна только тогда, когда изображения захватываются парой камер, жестко закрепленных относительно друг друга. Если одна камера захватывает изображения с двух разных углов, то мы можем найти глубину только в масштабе. Абсолютная глубина неизвестна, если у нас нет специальной геометрической информации о захваченной сцене, которую можно использовать для определения фактического масштаба.

На рисунке 5 показаны различные совпадающие точки, отмеченные вручную. Нам легко определить соответствующие точки, но как заставить компьютер это сделать?

Один из методов, который люди регулярно используют в сообществе компьютерного зрения, называется сопоставлением функций. На следующем рисунке 6 показаны совпадающие функции между левым и правым изображениями с использованием дескрипторов функций ORB. Это один из способов найти точечное соответствие (совпадение).

Однако мы наблюдаем, что отношение количества пикселей с известным точечным соответствием к общему количеству пикселей минимально. Это означает, что у нас будет очень редко реконструированная трехмерная сцена. Для плотной реконструкции нам нужно получить точечное соответствие для максимально возможного количества пикселей.

Упрощенный способ найти соответствия точек — это найти пиксели с аналогичной информацией о соседних пикселях. На рисунке 7 мы видим, что использование этого метода сопоставления пикселей с аналогичной информацией о соседях приводит к тому, что один пиксель из одного изображения имеет несколько совпадений в другом изображении.Нам сложно написать алгоритм для определения истинного соответствия.

Есть ли способ уменьшить пространство поиска? Некоторая теорема, которую мы можем использовать, чтобы исключить все лишние ложные совпадения, которые приводят к неточному соответствию? Здесь мы используем эпиполярную геометрию.

Все это объяснение и построение-до было ввести понятие эпиполярной геометрии. Теперь мы поймем важность эпиполярной геометрии для сокращения пространства поиска точечного соответствия.

Эпиполярная геометрия и ее использование в точечной корреспонденции

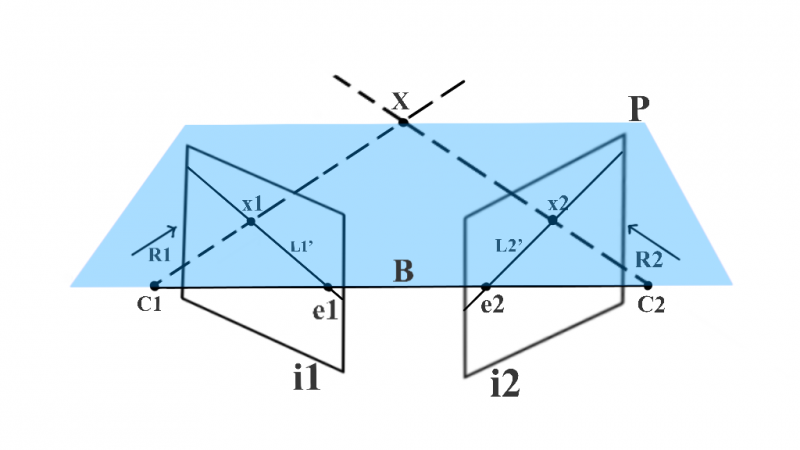
На рисунке 8 мы предполагаем установку, аналогичную рисунку 3. 3D-точка X снимается в точках x1 и x2 камерами в C1 и C2 соответственно. Поскольку x1 является проекцией X, если мы попытаемся удлинить луч R1 из C1, который проходит через x1, он также должен пройти через X. Этот луч R1 фиксируется как линия L2, а X фиксируется как x2 на изображении i2. Поскольку X лежит на R1,x2 должен лежать на L2. Таким образом, возможное местоположение x2 ограничено одной строкой, и, следовательно, мы можем сказать, что пространство поиска для пикселя в изображении i2, соответствующем пикселю x1, сокращается до одной строки L2. Мы используем эпиполярную геометрию, чтобы найти L2.

Пришло время определить некоторые технические термины! Наряду с X, мы также можем проецировать центры камеры на соответствующие противоположные изображения. e2 — это проекция центра камеры C1 на изображении i2, а e1 — это проекция центра камеры C2 на изображении i1. Технический термин для e1 и e2 — эпиполь. Следовательно, в настройке геометрии с двумя ракурсами эпиполь — это изображение центра камеры одного ракурса в другом ракурсе. Линия, соединяющая центры двух камер, называется базовой линией. Следовательно, эпиполь также можно определить как пересечение базовой линии с плоскостью изображения.

На рисунке 8 показано, что с помощью R1 и базовой линии мы можем определить плоскость P. Эта плоскость также содержит X, C1, x1, x2 и C2. Мы называем эту плоскость эпиполярной плоскостью. Более того,линия, полученная от пересечения эпиполярной плоскости и плоскости изображения, называется эпиполярной линией. Следовательно, в нашем примере L2 — эпиполярная линия. Для разных значений X у нас будут разные эпиполярные плоскости и, следовательно, разные эпиполярные линии. Однако все эпиполярные плоскости пересекаются на базовой линии,и все эпиполярные линии пересекаются в эпиполе. Все это вместе образует эпиполярную геометрию.

Вернемся к рисунку 8 со всеми техническими терминами, которые мы изучили до сих пор.

У нас есть эпиполярная плоскость P, созданная с использованием базовой линии B и луча R1. e1 и e2 — эпиполи, а L2 — эпиполярная линия. Исходя из эпиполярной геометрии данного рисунка,пространство поиска для пикселя в изображении i2, соответствующего пикселю x1, ограничено одной двумерной линией, которая является эпиполярной линией i2. Это называется эпиполярным ограничением.

Есть ли способ представить всю эпиполярную геометрию единой матрицей? Более того,можем ли мы рассчитать эту матрицу, используя только два захваченных изображения? Хорошая новость в том, что существует такая матрица, и она называется фундаментальной матрицей.

Далее станет понятно, что под проективной геометрией и однородным представлением мы подразумеваем, а затем попытаемся вывести фундаментальное матричное выражение. В заключение, вычисляем эпиполярные линии и представляем эпиполярное ограничение, используя фундаментальную матрицу.

Проективная геометрия и однородное представление

Как представить линию на двухмерной плоскости? Уравнение линии в 2D-плоскости: ax + by + c = 0. При разных значениях a, b и c мы получаем разные линии в 2D-плоскости. Следовательно, вектор (a, b, c) можно использовать для представления линии.

Предположим, что у нас есть линия ln1, определенная как 2x + 3y + 7 = 0, а линия ln2 как 4x + 6y + 14 = 0. На основе нашего вышеупомянутого обсуждения, l1 может быть представлен вектором (2,3,7), а l2 вектором (4,6,14). Мы можем легко сказать, что l1 и l2 по существу представляют одну и ту же линию, и что вектор (4,6,14) в основном является масштабированной версией вектора (2,3,7), масштабированной с коэффициентом 2.

Следовательно, любые два вектора (a, b, c) и k(a, b, c), где k — ненулевая масштабная константа, представляют собой ту же линию. Такие эквивалентные векторы, которые связаны только константой масштабирования, образуют класс однородных векторов. Вектор (a, b, c) является однородным представлением соответствующего ему эквивалентного класса векторов.

Набор всех эквивалентных классов, представленных (a, b, c), для всех возможных реальных значений a, b и c кроме a = b = c = 0, образует проективное пространство. Мы используем однородное представление однородных координат для определения таких элементов, как точки, линии, плоскости и т.д. В проективном пространстве. Мы используем правила проективной геометрии для выполнения любых преобразований этих элементов в проективном пространстве.

Получение фундаментальный матрицы

На рисунке 3 предположим, что мы знаем матрицы проекции камеры для обеих камер, скажем, P1 для камеры в C1 и P2 для камеры в C2.

Что такое матрица проекции? Матрица проекции камеры определяет соотношение между координатами трехмерного мира и соответствующими пиксельными координатами при захвате камерой. Чтобы узнать больше о матрице проекции камеры, прочитайте этот пост о калибровке камеры.

Точно так же, как P1 проецирует трехмерные мировые координаты в координаты изображения, мы определяем P1inv, псевдообратный к P1, так что мы можем определить луч R1 из C1, проходящий через x1 и X как:

X(k) = P1inv \times x1 + kC1

k — параметр масштабирования, так как мы не знаем фактического расстояния X от C1. Нам нужно найти эпиполярную линию Ln2, чтобы уменьшить пространство поиска для пикселя в i2, соответствующего пикселю x1 в i1, поскольку мы знаем, что Ln2 — это изображение луча R1, захваченное в i2. Следовательно, чтобы вычислить Ln2, мы сначала находим две точки на луче R1, спроецируем их на изображение i2 с помощью P2 и используйте проецируемые изображения двух точек, чтобы найти Ln2.

Первая точка, которую мы можем рассмотреть на R1, — это C1, так как луч начинается с этой точки. Вторую точку можно рассчитать, оставив k = 0. Следовательно, мы получаем точки как C1 и (P1inv) (x1). Используя матрицу проекции P2, мы получаем координаты этих точек на изображении i2 как P2 * C1 и P2 * P1inv * x1 соответственно. Мы также заметили, что P2 * C1 — это в основном эпиполь e2 на изображении i2.

Прямая может быть определена в проективной геометрии с использованием двух точек p1 и p2, просто найдя их векторное произведение p1 \times p2. Следовательно

Ln2 = P2 * C1 \times P2 * P1inv * x1

e2 = P2 * C1

при

Ln2 = e2 \times P2 * P1inv * x1

Для фундаментальной марицы

F = e2 \times P2 * P1inv

получим

Ln2 = F * x1

В проективной геометрии, если точка x лежит на прямой L, мы можем записать ее в виде уравнения

x^T \times L = 0

Следовательно, поскольку x2 лежит на эпиполярной прямой Ln2, получаем

x2^T \times Ln2 = 0

Заменяя значение Ln2 из приведенного выше уравнения, мы получаем уравнение:

x2^T \times F \times x1 = 0

Это необходимое условие для того, чтобы две точки x1 и x2 были соответствующими точками, и это также форма эпиполярного ограничения. Таким образом, F представляет собой общую эпиполярную геометрию системы с двумя точками зрения.

Что еще такого особенного в этом уравнении? Его можно использовать для поиска эпиполярных линий!

Использование фундаментальной матрицы для поиска эпиполярных линий

Поскольку x1 и x2 являются соответствующими точками в уравнении, если мы сможем найти соответствие для некоторых точек, используя методы сопоставления признаков, такие как ORB или SIFT, мы можем использовать их для решения вышеуказанного уравнения для F.

Метод findFundamentalMat() OpenCV предоставляет реализации различных алгоритмов, таких как алгоритм из 7 пунктов, алгоритм из 8 пунктов, алгоритм RANSAC и алгоритм LMedS для вычисления фундаментальной матрицы с использованием согласованных характерных точек.

Как только F известна, мы можем найти эпиполярную линию Ln2, используя формулу

Ln2 = F * x1

Если мы знаем Ln2, мы можем ограничить наш поиск пикселем x2, соответствующим пикселю x1, с помощью эпиполярного ограничения.

Частный случай двунаправленного зрения — параллельные плоскости изображения

Мы пытаемся решить проблему с перепиской. Мы начали с использования сопоставления признаков, но заметили, что это приводит к разреженной трехмерной структуре, поскольку известно точечное соответствие для крошечной доли от общего числа пикселей. Затем мы увидели, как можно использовать поиск на основе шаблонов для соответствия пикселей. Мы узнали, как можно использовать эпиполярную геометрию, чтобы сократить пространство поиска для соответствия точек до одной линии — эпиполярной линии.

Можем ли мы еще больше упростить процесс поиска плотных точечных соответствий?

На рисунках 9 и 10 показаны результаты сопоставления признаков и ограничение эпиполярной линии для двух разных пар изображений. В чем заключается наиболее существенная разница между двумя рисунками с точки зрения соответствия признаков и эпиполярных линий?

Да! Вы все правильно поняли! Соответствующие характерные точки имеют равные вертикальные координаты на рисунке 10. Все соответствующие точки имеют одинаковые вертикальные координаты. Все эпиполярные линии на рисунке 10 должны быть параллельны и иметь ту же вертикальную координату, что и соответствующая точка на левом изображении. Ну что в этом такого хорошего?

Точно! В отличие от случая, показанного на рисунке 9, нет необходимости явно рассчитывать каждую эпиполярную линию.Если пиксель на левом изображении находится в точке (x1, y1), уравнение соответствующей эпиполярной линии на втором изображении будет y = y1.

Мы ищем каждый пиксель в левом изображении для соответствующего ему пикселя в той же строке правого изображения. Это особый случай геометрии с двумя проекциями, когда плоскости изображения параллельны. Следовательно, эпиполи (изображение одной камеры, захваченное другой камерой) формируются на бесконечности. Основываясь на нашем понимании эпиполярной геометрии, эпиполярные линии встречаются в эпиполях. Следовательно, в этом случае, поскольку эпиполи находятся на бесконечности, наши эпиполярные линии параллельны.

Потрясающе! Это значительно упрощает проблему плотного точечного соответствия. Тем не мение,нам все еще нужно выполнить триангуляцию для каждой точки. Можем ли мы упростить и эту проблему? Что ж, еще раз, особый случай параллельных плоскостей изображения имеет для нас хорошие новости! Это помогает нам применять стереоразрыв. Это похоже на стереопсис или стереоскопическое зрение, метод, который помогает людям воспринимать глубину. Давайте разберемся в этом подробнее.

Что такое стереофоническое неравенство?

Следующий gif создан с использованием изображений из наборов стереоданных Миддлбери 2005. Он демонстрирует чистое поступательное движение камеры, делая плоскости изображения параллельными. Вы можете сказать, какие объекты ближе к камере?

Мы можем четко сказать, что игрушечная корова внизу находится ближе к камере, чем игрушки в верхнем ряду. Как мы это сделали? В основном мы видим сдвиг объекта на двух изображениях. Чем больше сдвигается объект ближе. Этот сдвиг мы называем неравенством. Как мы можем использовать это, чтобы избежать точечной триангуляции для вычисления глубины? Мы вычисляем диспаратность (сдвиг пикселя в двух изображениях) для каждого пикселя и применяем пропорциональное сопоставление, чтобы найти глубину для данного значения диспаратности. Это дополнительно подтверждается на рисунке 12.

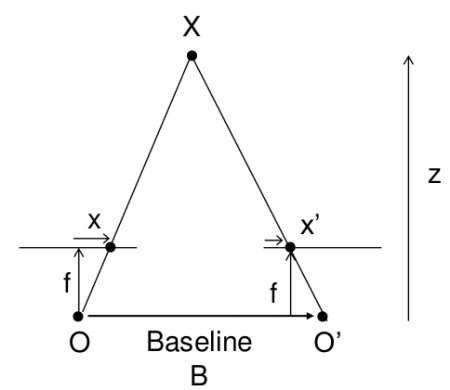
Disparity = x – x’ = \frac{Bf}{Z}

Где B — базовая линия (расстояние между камерами), а f — фокусное расстояние.

Мы будем использовать метод OpenCV StereoSGBM, чтобы написать код для вычисления карты диспаратности для данной пары изображений. Метод StereoSGBM основан на [3].

# Чтение левого и правого изображений.

imgL = cv2.imread("../im0.png",0)
imgR = cv2.imread("../im1.png",0)

# Настройка параметров для алгоритма StereoSGBM
minDisparity = 0;
numDisparities = 64;
blockSize = 8;
disp12MaxDiff = 1;
uniquenessRatio = 10;
speckleWindowSize = 10;
speckleRange = 8;

# Создание объекта алгоритма StereoSGBM
stereo = cv2.StereoSGBM_create(minDisparity = minDisparity,
        numDisparities = numDisparities,
        blockSize = blockSize,
        disp12MaxDiff = disp12MaxDiff,
        uniquenessRatio = uniquenessRatio,
        speckleWindowSize = speckleWindowSize,
        speckleRange = speckleRange
    )

# Вычисление диспарита с использованием алгоритма StereoSGBM
disp = stereo.compute(imgL, imgR).astype(np.float32)
disp = cv2.normalize(disp,0,255,cv2.NORM_MINMAX)

# Отображение карты диспаратности
cv2.imshow("disparity",disp)
cv2.waitKey(0)

Попробуйте поиграть с различными параметрами, чтобы увидеть, как они влияют на окончательный расчет карты несоответствия вывода. Подробное объяснение StereoSGBM будет представлено в следующей серии «Введение в пространственный ИИ». В следующем посте мы научимся создавать собственные настройки стереокамеры и записывать видео с картой несоответствия в реальном времени, кроме того, мы узнаем, как преобразовать карту диспаратности в карту глубины. Также будет объяснено интересное применение стереокамер, но это пока сюрприз!

Литература

[1] Richard Hartley and Andrew Zisserman. 2003. Multiple View Geometry in Computer Vision (2nd. ed.). Cambridge University Press, USA.

[2] D. Scharstein, H. Hirschmüller, Y. Kitajima, G. Krathwohl, N. Nesic, X. Wang, and P. Westling. High-resolution stereo datasets with subpixel-accurate ground truth. In German Conference on Pattern Recognition (GCPR 2014), Münster, Germany, September 2014.

[3] H. Hirschmuller, “Stereo Processing by Semiglobal Matching and Mutual Information,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 30, no. 2, pp. 328-341, Feb. 2008, doi: 10.1109/TPAMI.2007.1166.

По мотивам Introduction to Epipolar Geometry and Stereo Vision