В этом уроке мы узнаем, что такое дескриптор признаков гистограммы направленных градиентов (HOG). Мы узнаем, что находится под капотом и как этот дескриптор рассчитывается внутри OpenCVએ, MATLABએ и другими пакетами.
Этот пост является частью мини-курса из серии уроков, которые я пишу, о распознавании изображений и обнаружении объектов. Полный список уроков из этой серии приведен ниже:
- Распознавание изображений с использованием традиционных методов компьютерного зрения: часть 1
- Гистограмма направленных градиентов: часть 2
- Пример кода для распознавания изображений : часть 3
- Training a better eye detector: Part 4a
- Обнаружение объектов с использованием традиционных методов компьютерного зрения: часть 4b
- Как обучить и протестировать собственный детектор объектов OpenCV: Часть 5
- Распознавание изображений с использованием глубокого обучения: часть 6
- Обнаружение объектов с использованием глубокого обучения: часть 7
Многие вещи выглядят сложными и загадочными. Но как только вы потратите время на их изучение, тайна заменяется мастерством, и это то, что нам нужно. Если вы новичок и находите компьютерное зрение трудным и загадочным, просто запомните следующее.
Вопрос: Как съесть слона?
Ответ: По кусочкам!
Что такое дескриптор признаков?
Дескриптор признаков — это представление изображения или фрагмента изображения, которое упрощает изображение, извлекая полезную и отбрасывая бесполезную информацию.
Обычно дескриптор признака преобразует изображение размером ширина x высота x 3 (каналы) в вектор/массив признаков длиной n. В случае дескриптора признака HOG входное изображение имеет размер 64 \times 128 \times 3, а выходной вектор признака имеет длину 3 780.
Имейте в виду, что дескриптор HOG может быть рассчитан для других размеров, но в этом посте я придерживаюсь чисел, представленных в первоисточнике, чтобы вы легко могли понять концепцию на одном конкретном примере. Все это звучит хорошо, но что такое «полезное», а что «постороннее»? Чтобы определить «полезный», нам нужно знать, для чего он «полезен»? Ясно, что вектор признаков бесполезен для просмотра изображения. Но это очень полезно для таких задач, как распознавание изображений и обнаружение объектов. Вектор признаков, созданный этими алгоритмами, при подаче в алгоритмы классификации изображений, такие как метод опорных векторовએ (SVM), дает хорошие результаты.
Но какие «признаки» полезны для задач классификации? Давайте обсудим этот момент на примере. Предположим, мы хотим создать детектор объектов, который обнаруживает пуговицы на рубашках и пальто.
Пуговица имеет круглую форму (на изображении может выглядеть эллиптической) и обычно имеет несколько отверстий для пришивания. Вы можете запустить детектор края на изображении кнопки и легко определить, кнопка ли это, просто взглянув на изображение края. В этом случае информация о краях «полезна», а информация о цвете — нет. Кроме того, признаки также должны обладать отличительной способностью. Например, хорошие признаки, извлеченные из изображения, должны отличать кнопки от других круглых объектов, таких как монеты и автомобильные шины.
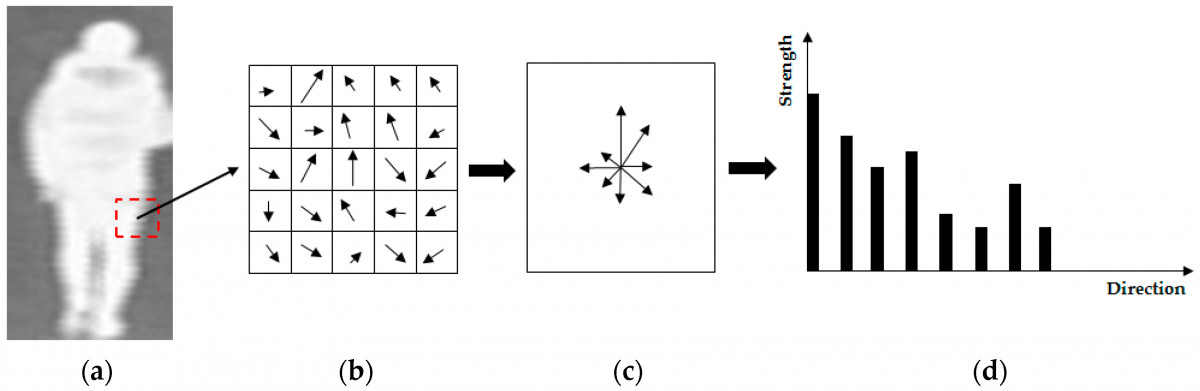
В дескрипторе признаков HOG в качестве признаков используются распределения (гистограммы) направлений градиентов (ориентированные градиенты). Градиенты (производные по x и y) изображения полезны, потому что величина градиентов велика по краям и углам (области резкого изменения интенсивности), и мы знаем, что края и углы содержат гораздо больше информации о форме объекта, чем плоские области.
Как рассчитать гистограмму ориентированных градиентов?
В этом разделе мы подробно рассмотрим расчет дескриптора функции HOG. Чтобы проиллюстрировать каждый шаг, мы будем использовать фрагмент изображения.
Шаг 1: предварительная обработка
Как упоминалось ранее, дескриптор функции HOG, используемый для обнаружения пешеходов, рассчитывается на участке изображения размером 64 \times 128 пикселей. Конечно, изображение может быть любого размера. Обычно пятна в нескольких масштабах анализируются во многих местах изображения. Единственное ограничение заключается в том, что анализируемые фрагменты имеют фиксированное соотношение сторон. В нашем случае, фрагменты должны иметь соотношение сторон 1:2. Например, они могут быть 100\:\times\:200, 128\:\times\:256 или 1000\:\times\:2000, но не 101\:\times\:205.
Чтобы проиллюстрировать этот момент, я показал большое изображение размером 720\:\times\:475. Мы выбрали фрагмент размером 100\:\times\:200 для вычисления нашего дескриптора признака HOG. Этот фрагмент вырезается из изображения и изменяется до 64\:\times\:128. Теперь мы готовы вычислить дескриптор HOG для этого фрагмента изображения.
В статье Далала и Триггса также упоминается гамма-коррекция как этап предварительной обработки, но прирост производительности незначительный, поэтому пропускаем этот этап.
Шаг 2: рассчитайте градиентные изображения
Чтобы вычислить дескриптор HOG, нам нужно сначала вычислить горизонтальный и вертикальный градиенты; ведь мы хотим вычислить гистограмму градиентов. Это легко достигается путем фильтрации изображения с помощью следующих ядер.
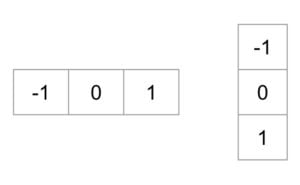
Мы также можем достичь тех же результатов, используя оператор Sobel из OpenCV с размером ядра 1.
# Прочитать изображение
im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0
# Рассчитать градиент
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
Затем мы можем найти величину и направление градиента, используя следующие уравнения:
g = \sqrt{g_x^2 + g_y^2}
\theta = \arctan{\dfrac{g_x}{g_y}}
Если вы используете OpenCV, расчет можно выполнить с помощью функции cartToPolar, как показано ниже.
# Вычислить величину и направление градиента (в градусах) mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
На рисунке ниже показаны градиенты.
Обратите внимание, что градиент g_x проявляется на вертикальных линиях, а градиент g_y виден на горизонтальных линиях. Вспышки величины градиентов везде, где наблюдается резкое изменение интенсивности. Ни градиент g_x, ни градиент g_y не наблюдаются на гладких областях. Я намеренно пропустил изображение, показывающее направление градиента, потому что направление, показанное как изображение, многого не передает.
Градиентное изображение удалило много несущественной информации (например, постоянный цветной фон), но выделило контуры. Другими словами, вы можете смотреть на градиентное изображение и все равно легко сказать, что на нем изображен человек.
В каждом пикселе градиент имеет величину и направление. Для цветных изображений оцениваются градиенты трех каналов (как показано на рисунке выше). Величина градиента в пикселе — это максимум величины градиентов трех каналов, а угол — это угол, соответствующий максимальному градиенту.
шаг 3: Вычислить гистограмму градиентов в ячейках 8 × 8
На этом этапе изображение делится на ячейки 8 × 8 и гистограмма градиентов вычисляется для каждой ячейки 8 × 8.
Мы узнаем о гистограммах через мгновение, но прежде чем мы перейдем к ним, давайте сначала поймем, почему мы разделили изображение на ячейки 8 × 8. Одна из важных причин использования дескриптора функции для описания фрагмента изображения заключается в том, что он обеспечивает компактное представление. Патч изображения 8 × 8 содержит значения 8 x 8 x 3 = 192 пикселей. Градиент этого патча содержит 2 значения (величину и направление) на пиксель, что в сумме дает 8 x 8 x 2 = 128 чисел. К концу этого раздела мы увидим, как эти 128 чисел представлены с использованием гистограммы с 9 ячейками, которую можно сохранить как массив из 9 чисел. Мало того, что представление более компактно, вычисление гистограммы по фрагменту делает это представление более устойчивым к шуму. На отдельных участках может быть шум, но гистограмма на участке 8 × 8 делает изображение менее чувствительным к шуму.
Но почему патч 8 × 8? Почему не 32 х 32? Это выбор дизайна, основанный на масштабах функций, которые мы ищем. Первоначально HOG использовался для обнаружения пешеходов. Ячейки 8 × 8 на фотографии пешехода в масштабе 64 × 128 достаточно велики, чтобы запечатлеть интересные черты (например, лицо, макушку и т. Д.).
Гистограмма представляет собой вектор (или массив) из 9 интервалов (чисел), соответствующих углам 0, 20, 40, 60 … 160.
Давайте посмотрим на один патч 8 × 8 на изображении и посмотрим, как выглядят градиенты.
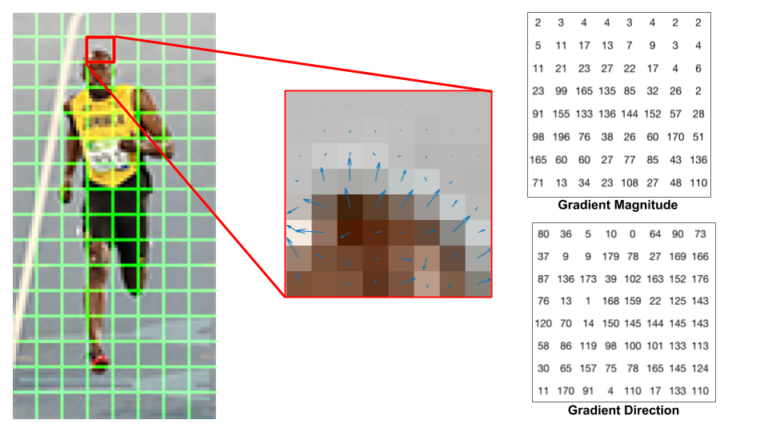
Если вы новичок в компьютерном зрении, изображение в центре будет очень информативным. Он показывает участок изображения, наложенный стрелками, показывающими градиент — стрелка показывает направление градиента, а ее длина показывает величину. Обратите внимание, как стрелки указывают направление изменения интенсивности, а величина показывает, насколько велика разница.
Справа мы видим необработанные числа, представляющие градиенты в ячейках 8 × 8 с одним незначительным отличием — углы составляют от 0 до 180 градусов вместо 0 до 360 градусов. Они называются «беззнаковыми» градиентами, потому что градиент и отрицательный градиент представлены одними и теми же числами. Другими словами, градиентная стрелка и стрелка на 180 градусов, противоположная ей, считаются одинаковыми. Но почему бы не использовать угол 0 — 360 градусов? Эмпирическим путем было показано, что градиенты без знака работают лучше, чем градиенты со знаком для обнаружения пешеходов. Некоторые реализации HOG позволят вам указать, хотите ли вы использовать подписанные градиенты.
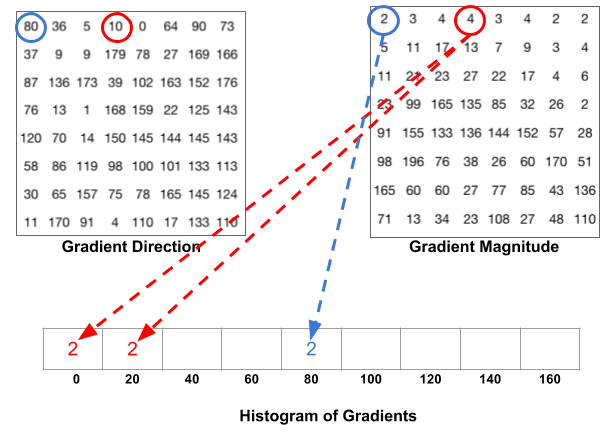
Следующим шагом будет создание гистограммы градиентов в этих ячейках 8 × 8. Гистограмма содержит 9 интервалов, соответствующих углам 0, 20, 40 … 160. На следующем рисунке показан процесс. Мы смотрим на величину и направление градиента того же участка 8 × 8, что и на предыдущем рисунке.
Бункер выбирается на основе направления, а голос (значение, которое попадает в корзину) выбирается на основе величины. Давайте сначала сосредоточимся на пикселе, обведенном синим. Он имеет угол (направление) 80 градусов и величину 2. Таким образом, он добавляет 2 к 5-му интервалу. Градиент в пикселе, обведенном красным, имеет угол 10 градусов и величину 4. Так как 10 градусов находятся на полпути между 0 и 20, голос пикселя равномерно распределяется на две ячейки.
Следует знать еще об одной детали. Если угол больше 160 градусов, он составляет от 160 до 180, и мы знаем, что угол оборачивается вокруг, делая 0 и 180 эквивалентами. Итак, в приведенном ниже примере пиксель с углом 165 градусов пропорционально вносит вклад в интервал 0 градусов и интервал 160 градусов.
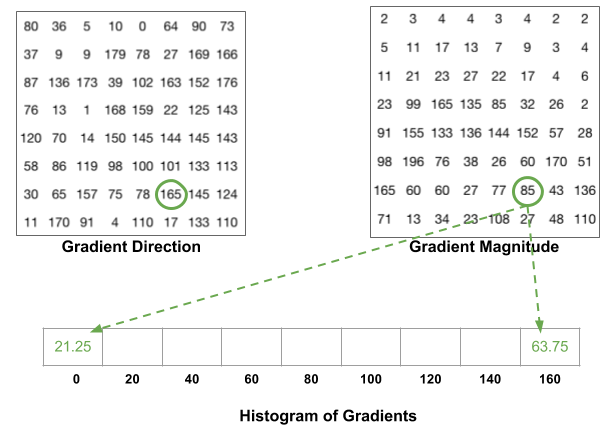
Вклады всех пикселей в ячейках 8 × 8 складываются для создания гистограммы с 9 ячейками. Для патча выше это выглядит так
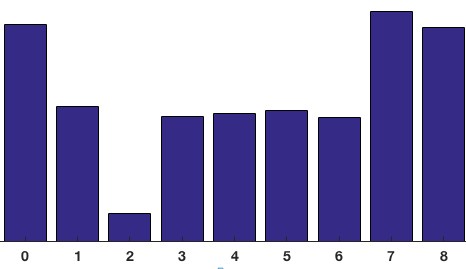
В нашем представлении ось Y равна 0 градусам. Вы можете видеть, что гистограмма имеет большой вес около 0 и 180 градусов, что является еще одним способом сказать, что градиенты в патче направлены вверх или вниз.
Шаг 4: Нормализация блока 16 × 16
На предыдущем шаге мы создали гистограмму на основе градиента изображения. Градиенты изображения чувствительны к общему освещению. Если сделать изображение темнее, разделив все значения пикселей на 2, величина градиента изменится вдвое, и, следовательно, значения гистограммы изменятся вдвое.
В идеале, мы хотим, чтобы наш дескриптор не зависел от вариаций освещения. Другими словами, мы хотели бы «нормализовать» гистограмму, чтобы на них не влияли изменения освещения.
Прежде чем я объясню, как нормализуется гистограмма, давайте посмотрим, как нормализуется вектор длины 3.
Допустим, у нас есть цветовой вектор RGB [128, 64, 32]. Длина этого вектора равна \sqrt{128^2 + 64^2 + 32^2} = 146,64. Это также называется L2-нормой вектора. Разделив каждый элемент этого вектора на 146,64, мы получим нормализованный вектор [0,87, 0,43, 0,22].
Теперь рассмотрим другой вектор, в котором элементы в два раза превышают значение первого вектора 2 x [128, 64, 32] = [256, 128, 64]. Вы можете сами решить, что нормализация [256, 128, 64] приведет к [0,87, 0,43, 0,22], что совпадает с нормализованной версией исходного вектора RGB. Вы можете видеть, что нормализация вектора удаляет масштаб.
Теперь, когда мы знаем, как нормализовать вектор,у вас может возникнуть соблазн подумать, что при вычислении HOG вы можете просто нормализовать гистограмму 9 × 1 так же, как мы нормализовали вектор 3 × 1 выше. Это неплохая идея, но лучше нормализовать по блоку большего размера 16 × 16. Блок 16 × 16 имеет 4 гистограммы, которые могут быть объединены, чтобы сформировать вектор элементов 36 x 1, и его можно нормализовать так же, как нормализован вектор 3 × 1. Затем окно перемещается на 8 пикселей (см. Анимацию), и для этого окна вычисляется нормализованный вектор размером 36 × 1, и процесс повторяется.
Шаг 5. Рассчитайте гистограмму вектора ориентированных градиентов.
Чтобы вычислить окончательный вектор признаков для всего фрагмента изображения, векторы размером 36 × 1 объединяются в один гигантский вектор. Каков размер этого вектора? Давайте посчитаем
- Сколько у нас позиций блоков 16 × 16? Есть 7 горизонтальных и 15 вертикальных позиций, что в сумме составляет 7 x 15 = 105 позиций.
- Каждый блок 16 × 16 представлен вектором 36 × 1. Итак, когда мы объединяем их все в один вектор затухания, мы получаем размерный вектор 36 × 105 = 3780.
Визуализация гистограммы ориентированных градиентов
Дескриптор HOG фрагмента изображения обычно визуализируется путем построения нормализованных гистограмм 9 × 1 в ячейках 8 × 8. См. Изображение сбоку. Вы заметите, что доминирующее направление гистограммы отражает форму человека, особенно вокруг туловища и ног.
К сожалению, нет простого способа визуализировать дескриптор HOG в OpenCV.
Литература:
Урок 2. Гистограмма направленных градиентов с использованием OpenCV, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Респект и уважуха
