Что такое искажение линз

В предыдущем посте мы рассмотрели геометрию формирования изображения и узнали, как точка в 3D проецируется на плоскость изображения камеры.

Модель, которую мы использовали, была основана на модели камеры-обскуры. Единственный раз, когда вы используете камеру-обскуру, вероятно, это во время затмения.

В модели формирования изображения любой реальной камеры используется объектив. Вы когда-нибудь задумывались, зачем мы прикрепляем объектив к нашим камерам? Влияет ли это на преобразование, определяющее проекцию трехмерных точек на соответствующий пиксель изображения? Если да, то как мы смоделируем это математически?

В этом посте мы ответим на поставленные выше вопросы.

Замена точечного отверстия линзой

Для получения четких и резких изображений диаметр апертуры (отверстия) камеры-обскуры должен быть как можно меньше. Если мы увеличим размер апертуры, мы знаем, что лучи из нескольких точек объекта будут падать на одну и ту же часть экрана, создавая размытое изображение.

С другой стороны, если мы сделаем размер диафрагмы маленьким, только небольшое количество фотонов попадет на датчик изображения. В результате изображение получается темным и зашумленным.

Таким образом, чем меньше апертура камеры-обскуры, тем более сфокусированным будет изображение, но в то же время оно темнее и шумнее.

С другой стороны, с большей апертурой, датчик изображения получает больше фотонов (и, следовательно, больше сигнала). Это приводит к яркому изображению с небольшим количеством шума.

Как получить четкое изображение, но в то же время захватить больше световых лучей, чтобы сделать изображение ярким?

Мы заменяем отверстие линзой, тем самым увеличивая размер отверстия, через которое могут проходить световые лучи. Линза позволяет большему количеству лучей проходить через отверстие и благодаря своим оптическим свойствам также может фокусировать их на экране. Это делает изображение ярче.

Потрясающе! Таким образом, мы получаем яркое и резкое, сфокусированное изображение с помощью линзы.

Проблема решена? Правильно? Не так всё быстро и просто. Ничего не дается бесплатно!

Основные эффекты искажений и их причины

Используя объектив, мы получаем изображения более высокого качества, но объектив вносит некоторые эффекты искажения. Есть два основных типа искажения:

1. Радиальное искажение: этот тип искажения обычно возникает из-за неравномерного отклонения света. Лучи изгибаются больше у краев линзы, чем лучи у центра линзы. Из-за радиального искажения прямые линии в реальном мире выглядят на изображении изогнутыми. Луч света смещается радиально внутрь или наружу от своего идеального местоположения, прежде чем попасть на датчик изображения. Есть два типа эффекта радиального искажения:
   1. Эффект деформации ствола, соответствующий отрицательному радиальному смещению
   2. Эффект деформации булавочной подушки, соответствующий положительному радиальному смещению.
2. Тангенциальное искажение: обычно возникает, когда экран изображения или датчик находится под углом к ​​объективу. Таким образом изображение кажется наклоненным и растянутым.

Согласно [1] существует 3 типа искажений в зависимости от источника искажения, радиального искажения, децентрализованного искажения и искажения тонкой призмы. Децентрализация и искажение тонкой призмы имеют эффект как радиального, так и тангенциального искажения.

Теперь у нас есть лучшее представление о том, какие типы эффектов искажения создает объектив, но как выглядит искаженное изображение? Стоит ли беспокоиться об искажении, которое вносит объектив? Если да, то почему? Как мы с этим справляемся?

На приведенном выше рисунке показан пример эффекта искажения, который может внести объектив. Вы можете связать рисунок 3 с рисунком 1 и сказать, что это эффект бочкообразного искажения, разновидность эффекта радиального искажения. Теперь, если вас попросят найти высоту правой двери,какие два момента вы бы рассмотрели? Все становится еще сложнее, когда вы выполняете SLAM или создаете какое-либо приложение дополненной реальности с камерами, имеющими большой эффект искажения изображения.

Математика искажений объектива

Когда мы пытаемся оценить трехмерные точки реального мира по изображению, нам необходимо учитывать эти эффекты искажения.

Мы математически моделируем эффект искажения на основе свойств объектива и комбинируем его с моделью камеры-обскуры, которая описана в предыдущем посте этой серии. Таким образом, наряду с внутренними и внешними параметрами, описанными в предыдущем посте, у нас также есть коэффициенты искажения (которые математически представляют искажение объектива) в качестве дополнительных внутренних параметров.

Чтобы учесть эти искажения в нашей модели камеры, мы модифицируем модель камеры-обскуры следующим образом:

\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}= \begin{bmatrix}R | T\end{bmatrix} \begin{bmatrix}X_w\\Y_w\\Z_w\end{bmatrix}

x' = \dfrac{X_c}{Z_c}

y' = \dfrac{Y_c}{Z_c}

\gamma = \dfrac{1 + K_1r^2 + K_2r^4 + K_3r^6}{1 + K_4r^2 + K_5r^4 + K_6r^6}

r^2 = x'^2 + y'^2

x'' = x'(\gamma) + 2P_1x'y' + P_2(r^2 + 2x'^2)

y'' = y'(\gamma) + P_1(r^2 + 2y'^2) + 2P_2x'y'

Матрица distCoeffs, возвращаемая методом calibrateCamera, дает нам значения от K_1 до K_6, которые представляют радиальное искажение и P_1, P_2, которые представляют тангенциальное искажение. Как мы знаем, приведенная выше математическая модель, представляющая искажение линзы, включает в себя все виды искажений, радиальные искажения, децентрализованное искажение и искажение тонкой призмы, таким образом, коэффициенты с K_1 по K_6 представляют чистое радиальное искажение, а P_1 и P_2 представляют чистое тангенциальное искажение.

Отлично! Итак, в этой серии постов о калибровке камеры мы начали с геометрии формирования изображения, затем выполнили калибровку камеры и обсудили основную теорию, а также обсудили математическую модель камеры с точечным отверстием, и, наконец, мы обсудили искажение объектива в этом посте. С этим пониманием теперь вы можете создать свою собственную виртуальную камеру и смоделировать некоторые интересные эффекты с помощью OpenCV^એ и Numpy^એ. Вы можете обратиться к этому репозиторию, где виртуальная камера реализована с использованием только Numpy. Имея в руках все параметры, как внутренние, так и внешние, вы можете лучше почувствовать влияние каждого параметра камеры на конечное изображение, которое вы видит

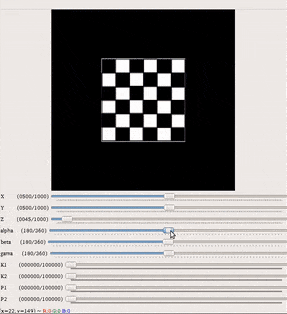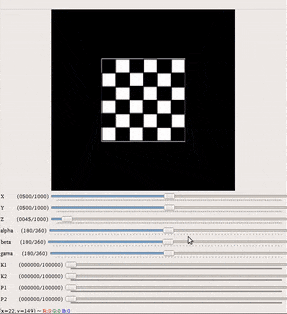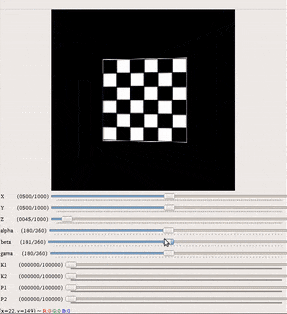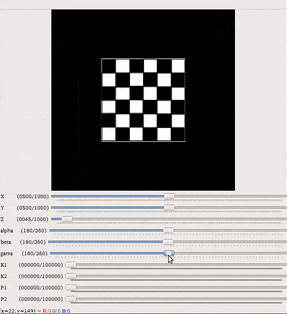
Gif, показывающий эффект вращения (слева), внешний параметр и эффект видимого размера пикселя (справа), внутренний параметр, с использованием моделирования виртуальной камеры.

Есть несколько других параметров, которые вы можете изменить с помощью графического интерфейса, предоставленного в репозитории. Это поможет вам лучше понять влияние различных параметров камеры.

Удаление искажения с помощью OpenCV

Итак, что нам делать после калибровки? Мы получили матрицу камеры и коэффициенты искажения в предыдущем посте о калибровке камеры, но как нам использовать значения?

Одно из приложений — использовать полученные коэффициенты искажения, чтобы не искажать изображение. На изображениях, показанных ниже, показано влияние искажения объектива и то, как его можно удалить из коэффициентов, полученных при калибровке камеры.

Есть три основных шага для устранения искажений, вызванных линзой.

1. Выполните калибровку камеры и получите внутренние параметры камеры. Это то, что мы сделали в предыдущем посте этой серии. К внутренним параметрам также относятся параметры искажения камеры.
2. Уточните матрицу камеры, чтобы контролировать процент нежелательных пикселей в неискаженном изображении.
3. Использование усовершенствованной матрицы камеры для неискаженного изображения.

Второй шаг выполняется с помощью метода getOptimalNewCameraMatrix(). Что означает эта доработанная матрица и зачем она нам? См. Следующие изображения, на левом изображении вы видите несколько черных пикселей по краям. Это происходит из-за неискажения изображения. Иногда эти черные пиксели нежелательны в конечном неискаженном изображении. Таким образом, метод getOptimalNewCameraMatrix() возвращает уточненную матрицу камеры, а также ROI (область интереса), которую можно использовать для обрезки изображения так, чтобы исключить все черные пиксели. Процент удаляемых нежелательных пикселей контролируется параметром alpha, который передается в качестве аргумента методу getOptimalNewCameraMatrix().

Важно отметить, что иногда в случае сильных радиальных искажений использование getOptimalNewCameraMatrix() с альфа = 0 генерирует пустое изображение. Обычно это происходит из-за того, что метод плохо оценивает искажения по краям. В таких случаях вам необходимо повторно откалибровать камеру и обеспечить, чтобы больше изображений было снято с разными видами, близкими к границам изображения. Таким образом, для оценки искажения будет доступно больше выборок около границы изображения для улучшения оценки.

# Уточнение матрицы камеры с использованием параметров, полученных при калибровке
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

# Метод 1 устранения искажений изображение
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)

# Метод 2 устранения искажений изображение
mapx,mapy=cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)

dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)

# Отображение неискаженного изображения
cv2.imshow("undistorted image",dst)
cv2.waitKey(0)

Литература

[1] J. Weng, P. Cohen, and M. Herniou. Camera calibration with distortion models and accuracy
evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(10):965–980,
Oct. 1992.

[2] Документация OpenCV для калибровки камер.

Источник вдохновения: Understanding Lens Distortion