Реализация алгоритма Дейкстры на Python

Что общего у устройств GPS‑навигации с веб‑сайтами для бронирования рейсов? Оказывается, очень много! Во‑первых, обе технологии используют алгоритм Дейкстры для поиска кратчайшего пути.

В этой статье я познаколю вас с алгоритмом Дейкстры и покажу его простую реализацию на Python. После простого русского языка, на котором всё будет понятно, вы увидите, что кодирование на Python не представляет больших сложностей.

Что такое алгоритм Дейкстры?

В 1956 году у голландского программиста Эдсгера В. Дейкстры возникла практическая задача — найти самый короткий путь из Роттердама в Гронинген. Однако, он не просто сверился с картой для рассчёта расстояния, которые ему нужно было пройти, использую длину дорог. Вместо этого, Дейкстра поступил, как информатик^એ: он абстрагировался от проблемы, отбросив такие мелочи, как путешествие из города А в город Б. Он сформулировал более общую проблему поиска по графу. Вот так и родился алгоритм Дейкстры^એ.

Алгоритм Дейкстры — это популярный алгоритм поиска, используемый для определения кратчайшего пути между двумя узлами в графе. В исходном сценарии граф представлял Нидерланды, узлы графа представляли разные голландские города, а рёбра представляли дороги между городами. Алгоритм Дейкстры можно использовать для решения любой задачи, которая может быть представлена в виде графа. Предложения друзей в социальных сетях, маршрутизация пакетов через Интернет или поиск пути через лабиринт — все это может сделать алгоритмом Дейкстры. Но как на самом деле это работает?

Напомним, что алгоритм Дейкстры для графов, а это означает, что он может решить проблему, только если она может быть представлена в графоподобном виде. Пример, который будет здесь показан, возможно, самый интуитивно понятный — кратчайший путь между двумя городами.

Мы будем работать с картой, показаной ниже, для поиска налучшего маршрута между двумя европейскими городами Рейкьявиком и Белградом. Для простоты представим, что все города связаны дорогами (реальный маршрут должен включать как минимум один паром).

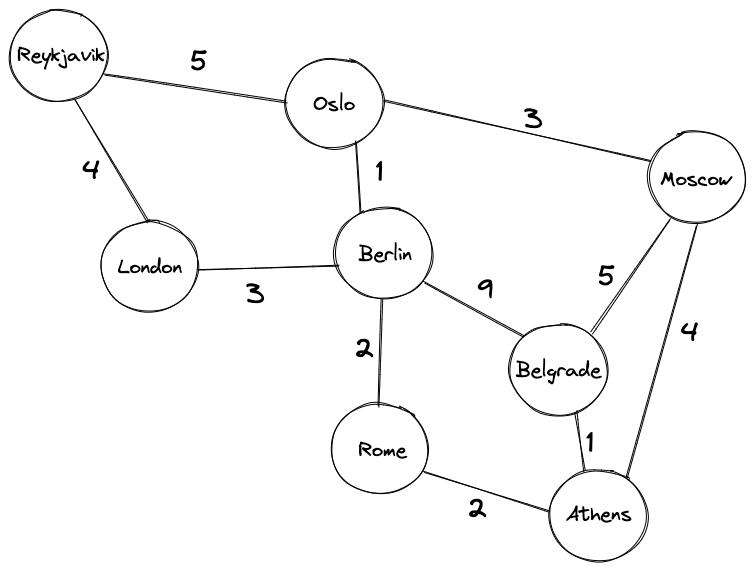
Обратите внимание на следующее:

Каждый город — это узел.
Каждая дорога — это ребро.
У каждой дороги есть своя ценность. Это может быть расстояние между городами, плата за проезд или интенсивностью движения. Как правило, мы отдаем предпочтение рёбрам с более низкими значениями. В нашем конкретном случае связанное значение определяется расстоянием между двумя городами.

Вы должны уже заметить, что добраться из Рейкьявика до Белграда напрямую невозможно. Это сделало бы наши упражнения бессмысленными. Но есть несколько путей из Рейкьявика в Белград, которые проходят через другие города:

Reykjavik → Oslo → Berlin → Belgrade
Reykjavik → London → Berlin → Rome → Athens → Belgrade
Reykjavik → London → Berlin → Rome → Athens → Moscow → Belgrade

Каждый из этих путей заканчивается в Белграде, но все они имеют разные ценности. Мы можем использовать алгоритм Дейкстры, чтобы найти путь с наименьшим общим значением.

Прежде чем погрузиться в код, посмотрим на алгоритм Дейкстры с высоты птичьего полета.

Сначала инициализируем алгоритм:

Устанавливаем Рейкьявик в качестве начального узла.
Устанавливаем расстояния между Рейкьявиком и всеми другими городами в ∞ (бесконечность), за исключением расстояния между Рейкьявиком и самим собой, которое принимаем равным 0.

После этого, итеративно выполняем следующие шаги:

Выбираем узел с наименьшим значением в качестве «текущего узла» и посещаем всех соседей. При посещении каждого соседа, обновляем их ориентировочное расстояние от начального узла.
Как только мы посетим всех соседей текущего узла и обновили их расстояния, помечаем текущий узел как «visited» «посещенный»). Отметка узла как «посещенного» означает, что найдена его окончательная ценность.
Вернемся к первому шагу и повторяем до тех пор, пока не посетим все узлы графа.

В нашем примере начинаем с отметки Рейкьявика, поскольку его значение равно 0, как «текущего узла». Далее посетим два соседних узла Рейкьявика: Лондон и Осло. В начале алгоритма их значения устанавливаются на бесконечность, но, когда мы посещаем узлы, то обновляем значение для Лондона до 4 и Осло до 5.

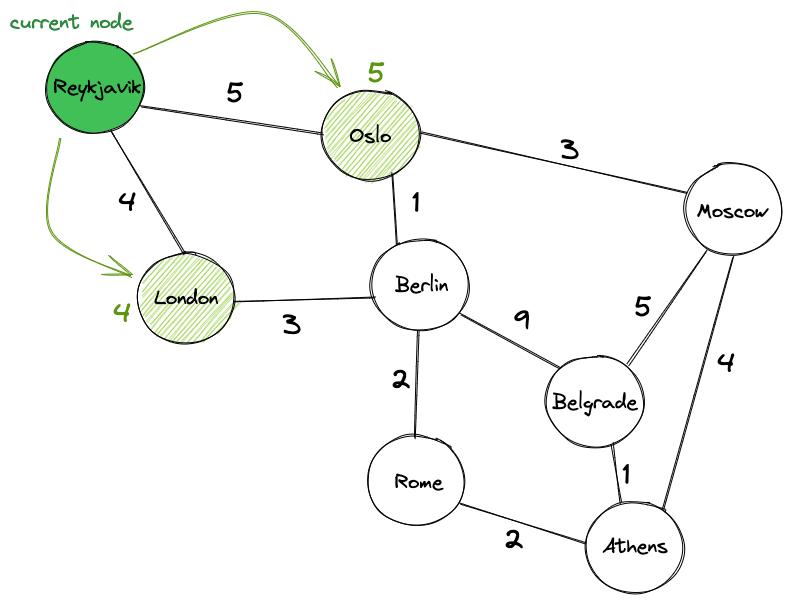
Затем отмечаем Рейкьявик как «посещенный». Мы знаем, что его окончательная стоимость равна нулю, и нам больше не нужно его посещать. Продолжаем со следующего узла с наименьшим значением, которым является Лондон.

Посещаем все соседние узлы Лондона, которые не помечены как «посещенные». Соседи Лондона — Рейкьявик и Берлин. Но мы игнорируем Рейкьявик, потому что мы уже были в нем. Вместо этого обновляем значение Берлина, добавляя значение ребра, соединяющего Лондон и Берлин (3), к значению Лондона (4), что дает нам значение 7.

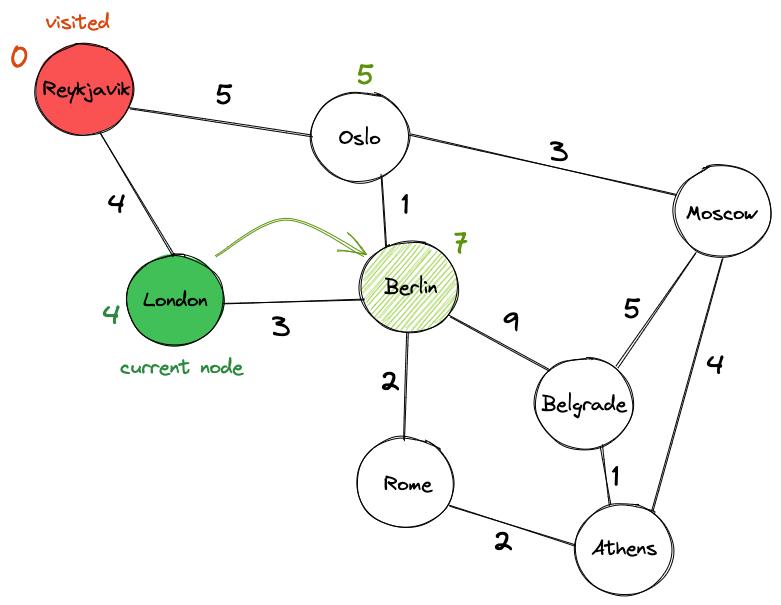
Отмечаем Лондон как посещенный и выбираем следующий узел — Осло. Посещаем соседей Осло и обновляем их ценности. Оказывается, можно лучше добраться до Берлина через Осло (со значением 6), чем через Лондон, поэтому соответствующим образом обновляем его значение. Также обновляем текущее значение Москвы с бесконечности до 8.

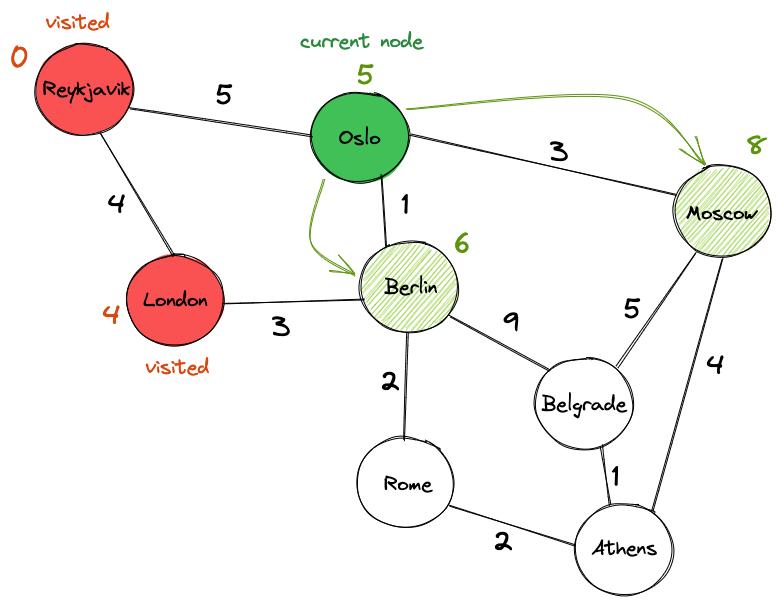
Отмечаем Осло как «посещенный» и обновляем его окончательное значение до 5. Между Берлином и Москвой выбираем Берлин в качестве следующего узла, потому что его значение (6) ниже, чем у Москвы (8). Действуем так же, как и раньше: посещаем Рим и Белград и обновляем их предварительные значения, прежде чем пометить Берлин как «посещенный» и перейти к следующему городу.

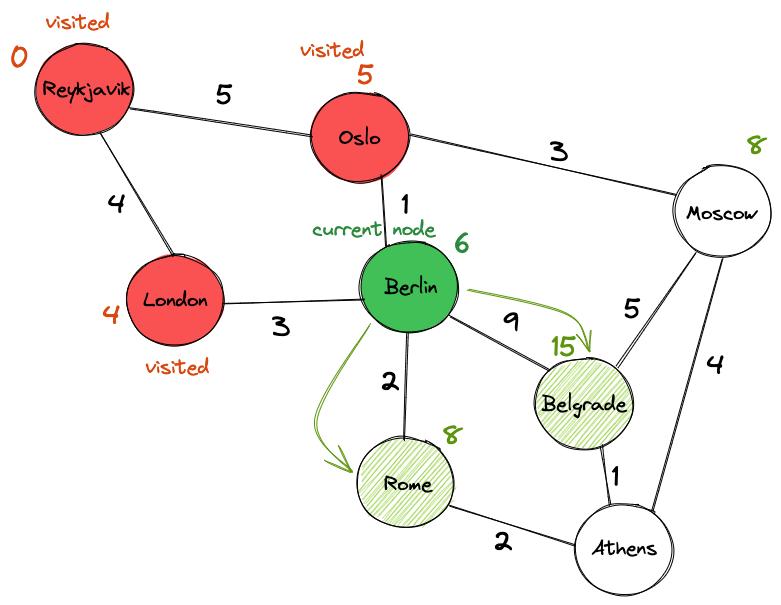
Обратите внимание, что мы уже нашли путь из Рейкьявика в Белград со значением 15! Но лучший ли он?

В конце концов, это не так. Пропустим остальные шаги, а для вас это упражнение. Лучшим путем оказывается Рейкьявик → Осло → Берлин → Рим → Афины → Белград со значением 11.

Теперь, посмотрим, как это реализовать на Python.

Алгоритм Дейкстры на Python

1) Класс Graph

Сначала создадим класс Graph. Этот класс не охватывает никакой логики алгоритма Дейкстры, но сделает реализацию алгоритма более лаконичной.

Реализуем граф как словарь Python. Ключи словаря будут соответствовать городам, а его значения будут соответствовать рёбрам, где записывают расстояния до других городов на графе.

import sys
 
class Graph(object):
    def __init__(self, nodes, init_graph):
        self.nodes = nodes
        self.graph = self.construct_graph(nodes, init_graph)
        
    def construct_graph(self, nodes, init_graph):
        '''
        Этот метод обеспечивает симметричность графика. Другими словами, если существует путь от узла A к B со значением V, должен быть путь от узла B к узлу A со значением V.
        '''
        graph = {}
        for node in nodes:
            graph[node] = {}
        
        graph.update(init_graph)
        
        for node, edges in graph.items():
            for adjacent_node, value in edges.items():
                if graph[adjacent_node].get(node, False) == False:
                    graph[adjacent_node][node] = value
                    
        return graph
    
    def get_nodes(self):
        "Возвращает узлы графа"
        return self.nodes
    
    def get_outgoing_edges(self, node):
        "Возвращает соседей узла"
        connections = []
        for out_node in self.nodes:
            if self.graph[node].get(out_node, False) != False:
                connections.append(out_node)
        return connections
    
    def value(self, node1, node2):
        "Возвращает значение ребра между двумя узлами."
        return self.graph[node1][node2]

2) Алгоритм Дейкстры

Далее реализуем алгоритм Дейкстры. Начнем с определения функции.

def dijkstra_algorithm(graph, start_node):

Функция принимает два аргумента: graph и start_node. graph — это экземпляр класса Graph, который мы создали на предыдущем шаге, тогда как start_node — это узел, с которого мы начнем вычисления. Мы вызовем метод get_nodes() для инициализации списка непосещенных узлов:

unvisited_nodes = list(graph.get_nodes())

Затем создадим два словаря, shorttest_path и previous_nodes:

Shorttest_path будет хранить наиболее известную стоимость посещения каждого города на графике, начиная с start_node. Вначале стоимость начинается с бесконечности, но мы будем обновлять значения по мере продвижения по графику.
previous_nodes будет хранить траекторию текущего наиболее известного пути для каждого узла. Например, если нам известен лучший способ добраться до Берлина через Осло, previous_nodes[«Берлин»] вернет «Осло», а previous_nodes[«Осло»] вернет «Рейкьявик». Мы будем использовать этот словарь, чтобы найти кратчайший путь.

shortest_path = {}
previous_nodes = {}
# Мы будем использовать max_value для инициализации значения "бесконечности" непосещенных узлов   
max_value = sys.maxsize
for node in unvisited_nodes:
    shortest_path[node] = max_value
# Однако мы инициализируем значение начального узла 0   
shortest_path[start_node] = 0

Теперь можно запустить алгоритм. Помните, что алгоритм Дейкстры выполняется до тех пор, пока не посетит все узлы в графе, поэтому представим это как условие выхода из цикла while.

while unvisited_nodes:

Теперь алгоритм может начать посещать узлы. Приведенный ниже блок кода сначала инструктирует алгоритм найти узел с наименьшим значением.

current_min_node = None
for node in unvisited_nodes: # Iterate over the nodes
    if current_min_node == None:
        current_min_node = node
    elif shortest_path[node] < shortest_path[current_min_node]:
        current_min_node = node

После этого алгоритм посещает всех соседей узла, которые еще не посещены. Если новый путь к соседу лучше, чем текущий лучший путь, алгоритм вносит корректировки в словари shorttest_path и previous_nodes.

# Приведенный ниже блок кода извлекает соседей текущего узла и обновляет их расстояния.
neighbors = graph.get_outgoing_edges(current_min_node)
for neighbor in neighbors:
    tentative_value = shortest_path[current_min_node] + graph.value(current_min_node, neighbor)
    if tentative_value < shortest_path[neighbor]:
        shortest_path[neighbor] = tentative_value
        # Мы также обновляем лучший путь к текущему узлу
        previous_nodes[neighbor] = current_min_node

После посещения всех его соседей мы можем пометить текущий узел как «посещенный»:

unvisited_nodes.remove(current_min_node

Наконец, мы можем вернуть два словаря:

return previous_nodes, shortest_path

3) Вспомогательная функция

Наконец, нам нужно создать функцию, которая печатает результаты. Эта функция будет принимать два словаря, возвращаемые функцией dijskstra_algorithm, а также имена начального и целевого узлов. Он будет использовать два словаря, чтобы найти лучший путь и сделать его оценку.

def print_result(previous_nodes, shortest_path, start_node, target_node):
    path = []
    node = target_node
    
    while node != start_node:
        path.append(node)
        node = previous_nodes[node]
 
    # Add the start node manually
    path.append(start_node)
    
    print("Найден следующий лучший маршрут {}.".format(shortest_path[target_node]))
    print(" -> ".join(reversed(path)))

Алгоритм в действии

Теперь посмотрим, как работает алгоритм. Dручную инициализируем узлы и их рёбра.

nodes = ["Reykjavik", "Oslo", "Moscow", "London", "Rome", "Berlin", "Belgrade", "Athens"]
 
init_graph = {}
for node in nodes:
    init_graph[node] = {}
    
init_graph["Reykjavik"]["Oslo"] = 5
init_graph["Reykjavik"]["London"] = 4
init_graph["Oslo"]["Berlin"] = 1
init_graph["Oslo"]["Moscow"] = 3
init_graph["Moscow"]["Belgrade"] = 5
init_graph["Moscow"]["Athens"] = 4
init_graph["Athens"]["Belgrade"] = 1
init_graph["Rome"]["Berlin"] = 2
init_graph["Rome"]["Athens"] = 2

Будем использовать эти значения для создания объекта класса Graph.

graph = Graph(nodes, init_graph)

Когда наш граф полностью построен, можно передать его функции dijkstra_algorithm().

previous_nodes, shortest_path = dijkstra_algorithm(graph=graph, start_node="Reykjavik")

А теперь распечатываем результаты:

print_result(previous_nodes, shortest_path, start_node="Reykjavik", target_node="Belgrade")

Вот и все! Не стесняйтесь экспериментировать с кодом. Например, можно добавить больше узлов к графу, настроить значения ребер или выбрать разные начальный и конечный города, считать города и расстояния из файла или базы данных.

Полный код приложения для проверки алгоритма Дейкстры

import sys
 
class Graph(object):
    def __init__(self, nodes, init_graph):
        self.nodes = nodes
        self.graph = self.construct_graph(nodes, init_graph)
        
    def construct_graph(self, nodes, init_graph):
        '''
        Этот метод обеспечивает симметричность графика. Другими словами, если существует путь от узла A к B со значением V, должен быть путь от узла B к узлу A со значением V.
        '''
        graph = {}
        for node in nodes:
            graph[node] = {}
        
        graph.update(init_graph)
        
        for node, edges in graph.items():
            for adjacent_node, value in edges.items():
                if graph[adjacent_node].get(node, False) == False:
                    graph[adjacent_node][node] = value
                    
        return graph
    
    def get_nodes(self):
        "Возвращает узлы графа"
        return self.nodes
    
    def get_outgoing_edges(self, node):
        "Возвращает соседей узла"
        connections = []
        for out_node in self.nodes:
            if self.graph[node].get(out_node, False) != False:
                connections.append(out_node)
        return connections
    
    def value(self, node1, node2):
        "Возвращает значение ребра между двумя узлами."
        return self.graph[node1][node2]

def dijkstra_algorithm(graph, start_node):
    unvisited_nodes = list(graph.get_nodes())
 
    # Мы будем использовать этот словарь, чтобы сэкономить на посещении каждого узла и обновлять его по мере продвижения по графику 
    shortest_path = {}
 
    # Мы будем использовать этот dict, чтобы сохранить кратчайший известный путь к найденному узлу
    previous_nodes = {}
 
    # Мы будем использовать max_value для инициализации значения "бесконечности" непосещенных узлов   
    max_value = sys.maxsize
    for node in unvisited_nodes:
        shortest_path[node] = max_value
    # Однако мы инициализируем значение начального узла 0  
    shortest_path[start_node] = 0
    
    # Алгоритм выполняется до тех пор, пока мы не посетим все узлы
    while unvisited_nodes:
        # Приведенный ниже блок кода находит узел с наименьшей оценкой
        current_min_node = None
        for node in unvisited_nodes: # Iterate over the nodes
            if current_min_node == None:
                current_min_node = node
            elif shortest_path[node] < shortest_path[current_min_node]:
                current_min_node = node
                
        # Приведенный ниже блок кода извлекает соседей текущего узла и обновляет их расстояния
        neighbors = graph.get_outgoing_edges(current_min_node)
        for neighbor in neighbors:
            tentative_value = shortest_path[current_min_node] + graph.value(current_min_node, neighbor)
            if tentative_value < shortest_path[neighbor]:
                shortest_path[neighbor] = tentative_value
                # We also update the best path to the current node
                previous_nodes[neighbor] = current_min_node
 
        # После посещения его соседей мы отмечаем узел как "посещенный"
        unvisited_nodes.remove(current_min_node)
    
    return previous_nodes, shortest_path

def print_result(previous_nodes, shortest_path, start_node, target_node):
    path = []
    node = target_node
    
    while node != start_node:
        path.append(node)
        node = previous_nodes[node]
 
   # Добавить начальный узел вручную
    path.append(start_node)
    
    print("Найден следующий лучший маршрут с ценностью {}.".format(shortest_path[target_node]))
    print(" -> ".join(reversed(path)))

nodes = ["Reykjavik", "Oslo", "Moscow", "London", "Rome", "Berlin", "Belgrade", "Athens"]
 
init_graph = {}
for node in nodes:
    init_graph[node] = {}
    
init_graph["Reykjavik"]["Oslo"] = 5
init_graph["Reykjavik"]["London"] = 4
init_graph["Oslo"]["Berlin"] = 1
init_graph["Oslo"]["Moscow"] = 3
init_graph["Moscow"]["Belgrade"] = 5
init_graph["Moscow"]["Athens"] = 4
init_graph["Athens"]["Belgrade"] = 1
init_graph["Rome"]["Berlin"] = 2
init_graph["Rome"]["Athens"] = 2

graph = Graph(nodes, init_graph)

previous_nodes, shortest_path = dijkstra_algorithm(graph=graph, start_node="Reykjavik")

print_result(previous_nodes, shortest_path, start_node="Reykjavik", target_node="Belgrade")

Мотиватор Implementing Dijkstra’s Algorithm in Python