Люди моего поколения ещё помнят то замечательное время, когда в каждом городском парке обязательно была комната смеха. Впервые в комнату смеха я попал году в 66-67 прошлого века на ВДНХ (Выставка достижений народного хозяйства, г. Москва) и с тех пор ни одна семейная прогулка в парке из моего детства не обходилась без этого развлечения. Конечно, весело было посмотреть на себя, но особенно на старших, как они молодели, становясь стройными и подтянутыми. Долго там делать нечего, но минут 15-20 безудержного, до слёз, смеха обеспечено.
С возрастом, конечно, беззаботность проходит. Примерно так, как в этой песне ансамбля «Ариэль»:
А в последнее время уже и не припомню, когда видел подобную комнату, представляющую собой небольшой павильонએ с развешенными на стенах огромными, в человеческий рост, кривыми зеркалами. Видать старые побились, а новые не делают — дорого в стекле. Почему кривыми? Потому что зеркала были не плоскими, к которым все привыкли в ванной, а изогнутыми самым невероятным образом, ну, естественно, не свёрнутыми в трубочку. Вот именно эта кривизна и обеспечивает то отражение собственного «Я», которое у индивида с нормальной психикой вызывает массу положительных эмоций. У людей же с не здоровой психикой положительная реакция на своё искажённое изображение возникает не всегда, а наблюдать в такой комнате поведение животных, кошек и собак, особенно забавно… В их маленьких мозгах явно возникает когнитивный диссонанс, что является ярким свидетельством их сообразительности.
Навеяло, однако. А нельзя ли создавать собственные кривые зеркала, опираясь на современные информационные технологии, немного кодируя на Python и зная о существовании OpenCV? — Легко, и в этом уроке вы узнаете, как это сделать.
Если всё внимательно прочитаете и отрепетируете приведенные здесь скрипты, то сможете наслаждаться подобными забавными эффектами у себя дома, не пытаясь найти по близости «Комнату смеха», что абсолютно соответствует режиму самоизоляции, продолжающегося уже четвёртую неделю, месяц, одним словом. Цифровая версия кривых зеркал с OpenCV сделана на основе проекта и авторского проекта Kaustubh Sadekar .
«Записки преподавателя» читает большинство моих студентов, поэтому один из мотивов создания урока — необходимость показать, как абстракции математики тесно связаны с реальностью и могут приносить вполне ощутимую пользу, как формулы могут разнообразить нашу жизнь и приносить массу положительных эмоций. К концу урока вы сможете оценить этот факт, понять, что можно создать что-то действительно интересное, имея четкое представление об основах математической теории. В общем, пусть учебный отдел считает это конспектом дистанционной лекции в рамках дисциплины «Программирование».
Теория формирования изображений
Чтобы понять механику проецирования трехмерной точки из мировой системы координат в кадр изображения камеры, рекомендую предварительно прочитать мои предыдущие статьи Геометрия формирования изображений и Калибровка камеры с использованием с OpenCV.
Прочитали? — Теперь вы знаете, что уравнения, которые связывают трехмерную точку (X_w, Y_w, Z_w) в мировой системе координат с её проекцией в координатах изображения (u, v), выглядят следующим образом:
\begin{bmatrix}u'\\v'\\w'\end{bmatrix} = \mathbf{P} \begin{bmatrix} X_w\\ Y_w\\ Z_w \\ 1 \end{bmatrix}
u = \dfrac{u'}{w'} \\ v = \dfrac{v'}{w'}
Где \mathbf{P} — матрица проекции размером 3 × 4, состоящая из двух частей: 1) внутренней матрицы \mathbf{K}, которая содержит внутренние параметры и 2) внешнюю матрицу ([\mathbf{R}\mid\mathbf{t}]), которая является комбинацией матрицы вращения \mathbf{R} размером 3 × 3 и вектора преобразования \mathbf{t} размером 3 × 1 .
\mathbf{P} = \mathbf{K} \times [\mathbf{R} \mid \mathbf{t}]
Как всё это работает?
Весь наш проект можно разделить всего на три основных части:
- Создание виртуальной камеры.
- Создание кривой (зеркальной) поверхности и проецирование на неё виртуальной камеры с использование подходящей математической абстракции — матрицы проекций.
- Используя сетку и координаты проецируемых точек на кривой поверхности, деформируем изображение для получения желаемого зеркального эффекта.
Надеюсь, рисунок поможет вам понять это лучше.

Если вы всё ещё ничего не поняли, не огорчайтесь. Далее каждую часть объясню подробно.
Создание виртуальной камеры
Основываясь на вышеупомянутой теории, мы четко знаем, как 3D‑точка в мировой системе координат связана с соответствующими координатами изображения.
Что же такое виртуальная камера и как делать снимки с этой виртуальной камерой?
Виртуальная камера — это, по сути, матрица P, которая описывает связь между трехмерными мировыми координатами и соответствующими пиксельными координатами изображения. Посмотрим, как мы можем создать свою виртуальную камеру с помощью Python.
Сначала создадим матрицу внешних параметров M1, матрицу внутренних параметров K и используем их для создания матрицы проекции камеры P.
import numpy as np # Определение матрицы перевода # Tx, Ty, Tz определяют положение виртуальной камеры в мировой системе координат T = np.array([ [1,0,0,-Tx],[0,1,0,-Ty],[0,0,1,-Tz] ]) # Определение матрицы вращения # alfa, beta, gamma определяют ориентацию виртуальной камеры Rx = np.array([ [1, 0, 0], [0, math.cos(alpha), -math.sin(alpha)], [0, math.sin(alpha), math.cos(alpha)] ]) Ry = np.array([ [math.cos(beta), 0, -math.sin(beta)],[0, 1, 0],[math.sin(beta),0,math.cos(beta)] ]) Rz = np.array([ [math.cos(gamma), -math.sin(gamma), 0],[math.sin(gamma),math.cos(gamma), 0],[0, 0, 1] ]) R = np.matmul(Rx, np.matmul(Ry, Rz)) # Расчет матрицы параметров внешней камеры M1 M1 = np.matmul(R,T) # Расчет матрицы параметров внутренней камеры K # sx и sy - кажущаяся длина пикселя по x и y # ox и oy - координаты оптического центра в плоскости изображения. K = np.array([ [-focus/sx,sh,ox],[0,focus/sy,oy],[0,0,1] ]) P = np.matmul(K,RT)
Обратите внимание, что необходимо устанавливать нужные значения для всех параметров focus, sx, sy, ox, oy и т.д.
Прочитайте эти статьи о том, как определить фокусное расстояние и как
Итак, как мы сможем захватить изображения с помощью этой виртуальной камеры?
Для начала предположим, что исходное изображение или видеокадр есть плоскость в 3D. Конечно, мы понимаем, что сцена на самом деле не является плоской, но у нас нет понимания глубины каждого пикселя изображения. Здесь мы просто делаем допущение, что сцена плоская, постольку-поскольку наша цель состоит не в точном моделировании кривого зеркала для научных исследование. Мы просто хотим немного развлечься.
После такого допущения мы можем просто умножить матрицу P на мировые координаты и, таким образом, получить координаты пикселей (u,v). Применение этого преобразования аналогично захвату изображения из трехмерных точек с помощью нашей виртуальной камеры!
А как мы решим вопрос с цветом пикселей в нашем захваченном изображении? А как насчет свойств материала объектов в сцене?
Всё вышеперечисленное определенно важно при рендеринге реалистичной 3D‑сцены, но нам не нужно рендерить реалистичную сцену. Мы просто развлекаемся.
Все, что нам нужно сделать, это захватить исходное изображение или видеокадр и представить его в виде трехмерной плоскости виртуальной камеры, а затем спроецировать каждую точку этой плоскости на кривую поверхность зеркала, используя матрицу проекции.
Как нам это сделать? Наивно было бы использовать цикл for и ещё один вложенный в него цикл for по всем точкам для этого преобразования. Такие вычисления в Python слишком накладны.
Поэтому, для подобных вычислений будем использовать numpy. Возможно, вы знаете, что позволяет выполнять векторизованные операции и устраняет необходимость использования циклов. Такие вычисления очень эффективны в сравнении с вложенными циклами for.
Таким образом, мы будем хранить трехмерные координаты в виде числового массива W, сохранять матрицу камеры в виде числового массива P и выполнять умножение матрицы P \times W для захвата трехмерных точек.
Вот и все!
Перед тем, как написать код захвата трехмерного изображения с помощью виртуальной камеры, необходимо определить кривую поверхность для моделирования зеркала.
Определение кривой поверхности (зеркала)
Для определения кривой поверхности формируем сетку из координат X и Y, а затем вычисляем координату Z как функцию от (X, Y) для каждой точки. Следовательно, для поверхности зеркала мы определим Z = K, где K — любая постоянная. На следующих рисунках показаны примеры некоторых зеркальных поверхностей, которые можно создавать.
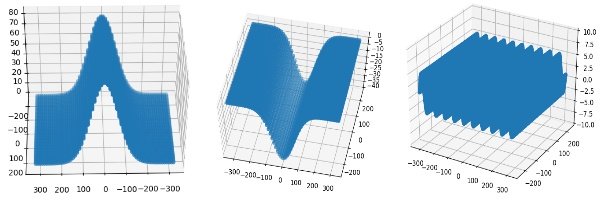
Теперь, когда у нас есть четкое представление о том, как определить кривую поверхность и захватить ее на нашей виртуальной камере, давайте посмотрим, как ее кодировать на python.
# Определить высоту и ширину входного изображения H,W = image.shape[:2] # Определить значения координат x и y в диапазоне (от -W/2 до W/2) и (от -H/2 до H/2) соответственно x = np.linspace(-W/2, W/2, W) y = np.linspace(-H/2, H/2, H) # Создание сетки с ячейками координатного диапазона x и y, определенного выше. xv,yv = np.meshgrid(x,y) # Генерация координат X, Y и Z плоскости # Здесь мы определяем плоскость Z = 1 X = xv.reshape(-1,1) Y = yv.reshape(-1,1) Z = X*0+1 # Сетка будет расположена в плоскости Z = 1 pts3d = np.concatenate(([X],[Y],[Z],[X*0+1]))[:,:,0] pts2d = np.matmul(P,pts3d) u = pts2d[0,:]/(pts2d[2,:]+0.00000001) v = pts2d[1,:]/(pts2d[2,:]+0.00000001)
Именно так мы создаём кривую поверхность для имитации кривого зеркала.
VCAM: виртуальная камера
Нужно ли писать вышеприведённый код каждый раз, когда мы захотим создать новое кривое зеркало? Что если надо динамически изменить некоторые параметры камеры? Для упрощения задачи создания кривых поверхностей, определения виртуальной камеры, установки всех параметров и нахождения их проекции, обратимся к библиотеке python под названием . В документации можно найти множество иллюстраций различных способов использования этой библиотеки, что облегчает создание виртуальных камер, определяя 3D‑точки и находя 2D‑проекции. Кроме того, эта библиотека заботится о настройке подходящих значений внутренних и внешних параметров и обрабатывает различные исключения, что делает её простой и удобной в использовании. Инструкции по установке библиотеки также находится в указанном репозитории.
Для установки библиотеки используйте .
pip3 install vcam
Вот как вы можете использовать библиотеку для написания кода, который работает аналогично коду, который мы написали до сих пор, но всего несколькими строками.
import cv2 import numpy as np import math from vcam import vcam,meshGen # Создать объект виртуальной камеры. Здесь H, W соответствуют высоте и ширине кадра входного изображения. c1 = vcam(H=H,W=W) # Создать объект поверхности plane = meshGen(H,W) # Изменить координату Z. По умолчанию Z установлен на 1 # Мы создаем зеркало, в котором для каждой трехмерной точки ее координата Z определяется как Z = 10 * sin (2 * pi [x/w] * 10) plane.Z = 10*np.sin((plane.X/plane.W)*2*np.pi*10) # Получить измененные 3D точки поверхности pts3d = plane.getPlane() # Спроецируйте 3D‑точки и получите соответствующие 2D‑координаты изображения, используя объект нашей виртуальной камеры c1 pts2d = c1.project(pts3d)
Можно легко увидеть, как библиотека vcam позволяет легко определять виртуальную камеру, создавать 3D‑поверхность и проецировать на неё захваченное изображение.
Теперь проецируемые 2D‑точки можно использовать для отражения на основе сетки. Это последняя часть создания нашего кривого зеркала.
Отражение изображения
Отражение — в нашем случае это создание нового изображения путем перемещения каждого пикселя входного изображения из его исходного местоположения на новое место, определенное функцией отражения. Таким образом, математически это записывается следующим образом:
I_{dst}(map_{x}(x,y),map_{y}(x,y)) = I_{src}(x,y)
Вышеприведенный метод называется переотражением вперед или деформированием вперед, где функции map_x и map_y дают нам новое положение пикселя, которое изначально было в (x, y).
Что делать, если map_x и map_y не дают нам целочисленное значение для конкретной пары (x, y)? Мы распространяем интенсивность пикселя в точке (x, y) на соседние пиксели, используя ближайшее целочисленное значение, что создает дыры в отражённом или результирующем изображении там, где пиксели, для которых интенсивность неизвестна и имеет значение 0. Как можно избежать такие дыры?
Используем обратную деформацию. Это значит, что теперь map_x и map_y предоставят нам старое положение пикселя в исходном изображении для заданного местоположения пикселя (x, y) в целевом изображении. Математически это выглядит так:
I_{dst}(x,y) = I_{src}(map_{x}(x,y),map_{y}(x,y))
Круто! Теперь мы знаем, как выполнить переотражение. Чтобы создать забавный зеркальный эффект, мы будем применять переотражение к исходному входному кадру. Но для этого нам нужны map_x и map_y, верно? Как мы определяем map_x и map_y в нашем случае? Ну, мы уже вычислили наши функции отображения.
2D проецируемые точки (pts2d), эквивалентные (u, v) в нашем теоретическом объяснении, являются желаемыми картами, которые мы можем передать функции переназначения. Теперь давайте посмотрим код для извлечения карт из проецируемых 2D точек и применения функции переотражения (деформации на основе сетки) для создания эффекта кривого зеркала.
# Получите mapx и mapy из 2-ых спроецированных точек
map_x,map_y = c1.getMaps(pts2d)
# Применение функции переотражения для входного изображения (img) и создания эффекта кривого зеркала
output = cv2.remap(img,map_x,map_y,interpolation=cv2.INTER_LINEAR)
cv2.imshow("Funny mirror",output)
cv2.waitKey(0)

Потрясающе! Попробуем создать еще одно кривое зеркало с удлинением середины по вертикали. После этого вы сможете делать свои собственные кривые зеркала.
import cv2 mport numpy as np
import math
from vcam import vcam,meshGen
# Чтение входного изображения. Передайте путь изображения, которое вы хотели бы использовать в качестве входного изображения.
img = cv2.imread("chess.png")
H,W = img.shape[:2]
# Создание объекта виртуальной камеры
c1 = vcam(H=H,W=W)
и
# Создание объекта поверхности
plane = meshGen(H,W)
# Мы создаем зеркало, в котором для каждой трехмерной точки ее координата Z определяется как Z = 20 * exp^((x/w)^2/2 * 0.1 * sqrt(2 * pi))
plane.Z += 20*np.exp(-0.5*((plane.X*1.0/plane.W)/0.1)**2)/(0.1*np.sqrt(2*np.pi))
pts3d = plane.getPlane()
pts2d = c1.project(pts3d)
map_x,map_y = c1.getMaps(pts2d)
output = cv2.remap(img,map_x,map_y,interpolation=cv2.INTER_LINEAR)
cv2.imshow("Funny Mirror",output)
cv2.imshow("Input and output",np.hstack((img,output)))
cv2.waitKey(0)

Итак, теперь, когда мы знаем, что, определяя Z как функцию от X и Y, мы можем создавать различные типы эффектов искажения. Давайте создадим еще несколько эффектов, используя приведенный выше код. Нам просто нужно изменить строку, в которой мы определяем Z как функцию (X, Y). Это поможет вам создать ваши собственные эффекты.
# Мы создаем зеркало, в котором для каждой трехмерной точки ее координата Z определяется как Z = 20 * exp^((y/h) ^ 2/2 * 0.1 * sqrt (2 * pi)) plane.Z += 20*np.exp(-0.5*((plane.Y*1.0/plane.H)/0.1)**2)/(0.1*np.sqrt(2*np.pi))

Давайте используем функцию sin!
# Мы создаем зеркало, в котором для каждой трехмерной точки ее координата Z определяется как Z = 20 * [sin (2 * pi * (x/w-1/4))) + sin (2 * pi * (y/h) -1/4)))] plane.Z += 20*np.sin(2*np.pi*((plane.X-plane.W/4.0)/plane.W)) + 20*np.sin(2*np.pi*((plane.Y-plane.H/4.0)/plane.H))

Входные (слева) и выходные (справа) изображения, показывающие эффект искажения, созданный с помощью вышеупомянутой функции для координаты Z кривой поверхности
Как насчет эффекта радиального искажения?
# Мы создаем зеркало, в котором для каждой трехмерной точки ее координата Z определяется как Z = -100*sqrt[(x/w)^2 + (y/h)^2] plane.Z -= 100*np.sqrt((plane.X*1.0/plane.W)**2+(plane.Y*1.0/plane.H)**2)

Входные (слева) и выходные (справа) изображения, показывающие эффект искажения, созданный с помощью вышеупомянутой функции для координаты Z кривой поверхности
Источником вдохновлен этого урока является созданный Kaustubh Sadekar. Там вы можете найти множество других интересных кривых зеркал. Однако, столкнувшись с некоторыми проблемами при создании своих кривых зеркал вам придётся применить знания математики и навыки творческого мышления для получения правильных решений. Количество различных зеркал, теперь ограничено только вашей креативностью и способностями визуализировать математику.
Идите вперед и создавайте свои собственные зеркала, поделитесь ими со своими близкими и раскрасьте положительными эмоциями утомительные дни дистанционного обучения в режиме самоизоляции
Источник вдохновения:
![]() Комната смеха во времена пандемии COVID-19, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Комната смеха во времена пандемии COVID-19, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Респект и уважуха


