Да, вы должны понимать, что такое обратное распространение

Когда в Стэнфорде появился курс CS231n (глубокое машинное обучение), то для него намеренно и специально были разработаны задания по программированию самого низкого уровня, включающие реальные вычисления, связанные с обратным распространением ошибок. Студенты должны были реализовать прямой и обратный проход каждого слоя в необработанном виде. Естественно, некоторые ученики неизбежно жаловались на доске объявлений в классе:

«Почему мы должны описывать обратный проход, когда в реальном мире есть фреймворки такие, как TensorFlow, которые вычисляют его автоматически?»

Кажется вполне разумно, на первый взгляд, что если после окончания курса вы никогда не собираетесь писать обратные проходы, то зачем в этом практиковаться? Преподаватели ради собственного развлечения мучают студентов? Некоторые простые ответы могут привести к аргументам типа «то, что скрывается под капотом есть бесполезная интеллектуальная мастурбация и надо ли этим заниматься» или «возможно, позже вы захотите улучшить основной алгоритм», однако, есть гораздо более сильный и практичный аргумент, которому я хотел бы посвятить целый пост:

> Проблема обратного распространения — очень даже неплохая концепция.

Другими словами, слишком много исследователей легко попадают в ловушку абстрагирования в процессе обучения, полагая, что можно просто складывать произвольные слои вместе, а обратное распространение «волшебным образом заставит их работать» с вашими данными. Итак, давайте рассмотрим несколько явных примеров, когда интуиция нас обманывает.

Градиенты, исчезающие на сигмоидах

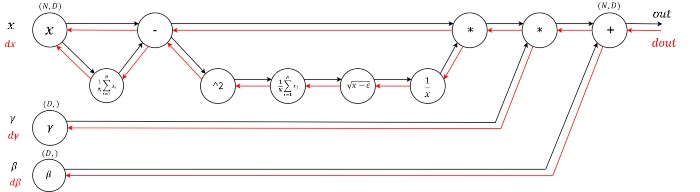
Здесь всё легко. В какой-то момент было модно использовать сигмовидную (или тангенциальную) нелинейность в полностью связанных слоях. Сложность, которую люди могут не понять, пока они не подумают об обратном проходе, заключается в том, что если вы небрежно настроили инициализацию веса или предварительную обработку данных, линейности могут «насытить» и полностью прекратить обучение — ваши потери в обучении будут постоянными и откажутся снижаться. Например, полностью связанный слой с сигмоидной нелинейностью вычисляет (с использованием raw numpy):

z = 1/(1 + np.exp(-np.dot(W, x))) # прямой проход
dx = np.dot(W.T, z*(1-z)) # обратный проход: локальный градиент для x
dW = np.outer(z*(1-z), x) # обратный проход: локальный градиент для W

Если ваша матрица весов W инициализирована слишком большой, результат умножения матрицы может иметь очень большой диапазон (например, числа от -400 до 400), что сделает все выходные данные в векторе z почти двоичными: либо 1, либо 0. Но если это так, z\,\times\,(1-z), который является локальным градиентом сигмовидной нелинейности, в обоих случаях станет равным нулю («исчезнет»), сделав градиент для x и W равным нулю. Остальная часть обратного прохода с этого момента будет иметь все нули из-за умножения в правиле цепочки.

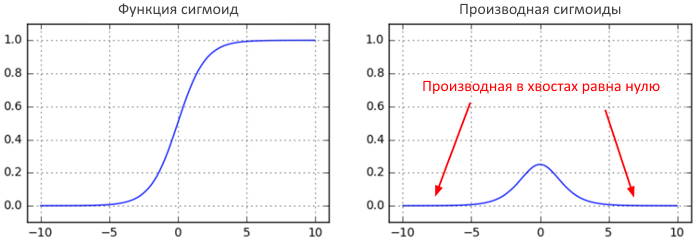
Другой неочевидный и забавный факт о сигмоиде заключается в том, что его локальный градиент (z\,\times\,(1-z)) достигает максимума при 0,25, когда z = 0,5. Это означает, что каждый раз, когда сигнал градиента проходит через сигмовидный вентиль, его величина всегда уменьшается на четверть (или более). Если вы используете в качестве базового стохастический градиентный спуск^એ (SGD), то нижние уровни сети будут намного медленнее, чем верхние.

Если вы в своей сети используете сигмоиды или тангенциальные нелинейности и понимаете обратное распространение, вам всегда следует беспокоиться о том, чтобы инициализация не приводила к их полному насыщению. См. Более подробное объяснение в видео лекции CS231n.

Умирающие ReLU

Еще одна забавная нелинейность — это ReLU, которая ограничивает нейроны нулевым порогом снизу. Прямой и обратный проход для полностью подключенного уровня, использующего ReLU в ядре, будет включать:

z = np.maximum(0, np.dot(W, x)) # прямой проход
dW = np.outer(z > 0, x) # обратный проход: локальный градиент для W

Если какое-то время вы будете на это смотреть, то увидите, что фиксированном в нуле нейроне прямом проходе (то есть z = 0, он не «срабатывает», потому как его веса будут иметь нулевой градиент. Это может привести к так называемой проблеме «мертвого ReLU», когда, если нейрон ReLU, к сожалению, инициализирован так, что он никогда не срабатывает, или если веса нейрона когда-либо будут сбиты с большим обновлением во время обучения в этом режиме, то этот нейрон навсегда останется мертвым. Это как необратимое повреждение мозга. Иногда вы можете переслать весь обучающий набор через обученную сеть и обнаружить, что большая часть (например, 40%) ваших нейронов все время были нулевыми.

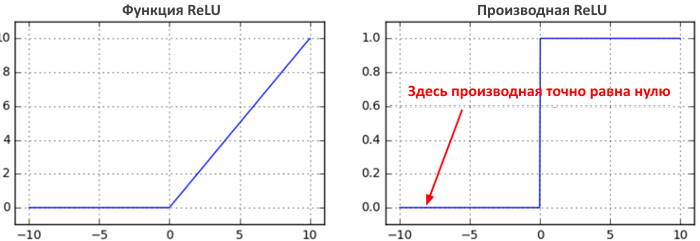
Если вы понимаете обратное распространение и в вашей сети есть ReLU, то всегда нервничаете по поводу мертвых ReLU. Это нейроны, которые никогда не включаются ни в одном примере во всей вашей обучающей выборке и навсегда останутся мертвыми. Нейроны также могут погибнуть во время тренировки, как правило, из-за агрессивной скорости обучения. См. Более подробное объяснение в видео лекции CS231n.

Взрывные градиенты в RNN

Ванильные RNN^એ представляют собой еще один хороший пример неинтуитивных эффектов обратного распространения ошибки. Я скопирую и вставлю слайд из CS231n, который имеет упрощенную RNN, которая не принимает никакого ввода x и вычисляет только повторение в скрытом состоянии (эквивалентно, вход x всегда может быть равен нулю):

Эта RNN разворачивается за T временных шагов. Когда вы посмотрите на то, что делает обратный проход, вы увидите, что сигнал градиента, идущий назад во времени через все скрытые состояния, всегда умножается на одну и ту же матрицу (матрицу повторения Whh), перемежающуюся обратным распространением нелинейности. Что произойдет, если вы возьмете одно число a и начнете умножать его на другое число b (т.е. a\,\times\,b\,\times\,b\,\times\,b\,\times\,b\,\times\,b\,\times\,b \dots)? Эта последовательность либо стремится к нулю, если |b| < 1, или улетает в бесконечность, когда |b| > 1. То же самое происходит при обратном проходе RNN, за исключением того, что b — это матрица, а не просто число, поэтому вместо этого мы должны рассуждать о его наибольшем собственном значении.

Если вы понимаете обратное распространение и используете RNN, то беспокоитесь о том, что придется выполнять градиентную обрезку, или вы предпочитаете использовать LSTM^એ. См. Более подробное объяснение в видео лекции CS231n.

Замечено в дикой природе: вырезка из DQN

Давайте посмотрим на еще один — тот, который на самом деле вдохновил этот пост. Вчера я просматривал реализацию Deep Q Learning в TensorFlow (чтобы увидеть, как другие справляются с вычислением числового эквивалента Q[:, a], где a — целочисленный вектор — оказалось, что эта тривиальная операция не поддерживается в TF). В любом случае, я поискал «dqn tensorflow», щелкнул первую ссылку и нашел основной код. Вот отрывок:

Если вы знакомы с DQN, вы можете видеть, что есть target_q_t, который представляет собой просто [reward * \gamma \argmax_a Q(s’,a)], а затем есть q_hibited, который равен Q(s, a) о предпринятых действиях. Здесь авторы вычитают два в переменную дельту, которую они затем хотят минимизировать в строке 295 с помощью потери L2 с помощью tf.reduce_mean(tf.square ()). Все идет нормально.

Проблема находится в строке 291. Авторы стараются быть устойчивыми к выбросам, поэтому, если дельта слишком велика, они обрезают ее с помощью tf.clip_by_value. Это сделано из лучших побуждений и выглядит разумным с точки зрения прямого прохода, но вносит серьезную ошибку, если вы думаете об обратном проходе. Функция clip_by_value имеет локальный нулевой градиент за пределами диапазона от min_delta до max_delta, поэтому всякий раз, когда дельта превышает min/max_delta, градиент становится точно нулевым во время обратного распространения. Авторы обрезают необработанную дельту Q, когда они, вероятно, пытаются обрезать градиент для дополнительной надежности. В этом случае правильнее будет использовать потерю Хубера вместо tf.square:

def clipped_error(x): 
  return tf.select(tf.abs(x) < 1.0, 
                   0.5 * tf.square(x), 
                   tf.abs(x) - 0.5) # условие, истина, ложь

В TensorFlow^એ это сделано грубовато. Всё, что мы хотим сделать, это обрезать градиент, если он выше порогового значения, но поскольку мы не можем напрямую вмешиваться в градиенты, мы должны делать это таким кружным путём определения потерь Хубера. В Torch^એ это было бы намного проще.

Я представил проблему в репо DQN и она была быстро исправлена.

В заключении

Обратное распространение - это ненадежная абстракция; это схема присвоения кредита с нетривиальными последствиями. Если вы попытаетесь игнорировать то, как это работает под капотом, потому что «TensorFlow автоматически заставляет мои сети учиться», вы не сможете победить опасности, доверяясь ему и будете гораздо менее эффективны при построении и отладке нейронных сетей.

Хорошая новость заключается в том, что обратное распространение не так сложно понять, если оно представлено правильно. У меня относительно сильные чувства по этой теме, потому что мне кажется, что 95% материалов по обратному распространению представляют все это неправильно, основываясь на огромном количестве страниц с формальной математикой. Вместо этого я бы порекомендовал лекцию CS231n об обратном распространении информации, которая подчеркивает интуицию (ура! бесстыдной саморекламе). А если у вас есть время, в качестве бонуса поработайте над заданиями CS231n, которые заставят вас писать обратную связь вручную и помогут закрепить полученные знания. На этом пока все! Надеюсь, вы с большим подозрением отнесетесь к обратному распространению, идущему вперед, и тщательно продумайте, что делает обратный проход. Кроме того, мне известно, что этот пост (непреднамеренно!) Превратился в несколько объявлений CS231n. Извиняюсь за это 🙂

Перевод Yes you should understand backprop